二次関数の最大値・最小値／関数が固定されて区間（定義域）が動く場合

二次関数の最大値・最小値／区間（定義域）が固定されて軸が動く場合　からの続き

今回は関数が固定されて区間が動く場合の二次関数の最大値・最小値の求め方について説明します。

区間（定義域）が固定されて関数の軸が動く場合と並んでとても重要な問題です。

区間、関数の軸どちらを動かされても確実に解けるようになることが目標です。

区間が動く場合の最大値・最小値を求める手順

考える手順は前回の区間固定の時と同様です。

①平方完成する
②軸、区間など何が動いて何が動かないのか確認する
③動かないものをとりあえず図示
④③をした上で動くものを動かしてどこで場合分けするか考える
⑤場合分けしたらそれぞれの場合ごとに図を書いて最大値・最小値を取る場所を求める。

この手順を頭に入れた上で例題を通して解き方を見ていきましょう。

例題

関数ｙ＝ｘ^２−５ｘ＋６
（ａ≦ｘ≦ａ＋４）の
最大値、最小値を求めよ。

---

解答：
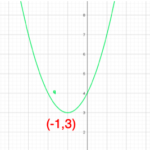
与えられた式を平方完成すると

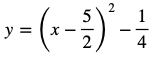
です。

次に今回動くものがあるのか、何が動くのかを確認していきます。

動くか動かないかは「文字になっているか、具体的な数字になっているか」で大体見分けられます。

ということで今回は区間だけが動いて関数のグラフは動かないことが分かります。

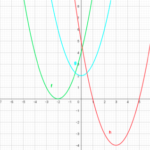
動かないもの（関数のグラフ）の図を書くと次のようになります。

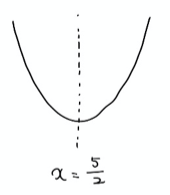
次はこの図を使って、動くもの（区間）をいろんな位置にとってどこで場合分けが必要かを考えます。

今回は区間の”幅”は一定で位置だけ変わるので、それを念頭に考えていきます。

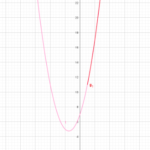
このステップは言葉で説明するとややこしくなるので、細かく図にしていきながら、最大値最小値を考えます。

---

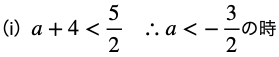
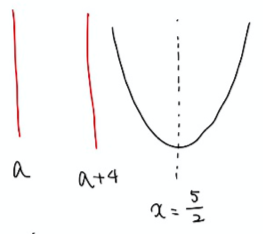
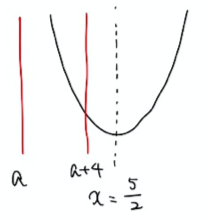
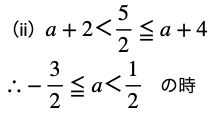
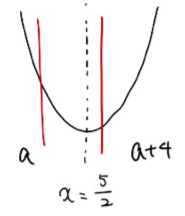
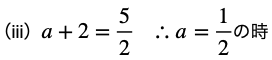
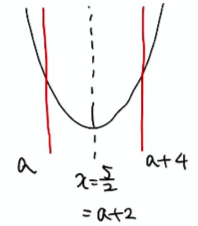
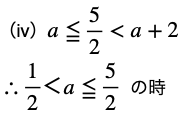
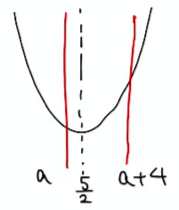
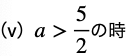
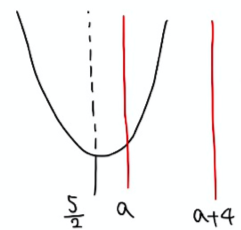
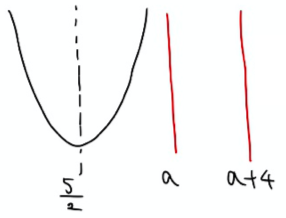
あくまで最大値と最小値は分けて考えるのが基本なので慣れないうちは最大値と最小値で別々に考えた方がいいです。

しかしある程度慣れてくればこのように一気に考えるとスマートな答えが書けます。

この例からも分かってもらえるかと思いますが、数学は実験しないとどうしようもない問題が数多く存在します。

二次関数の最大値・最小値も動くものが出てきたら焦らず図を書いて、丁寧に調べていけば自ずと場合分けの仕方は見えていきます。

軸や区間（定義域）が動く二次関数の最大値最小値まとめ

この単元に限らず場合分けを苦手とする高校生は非常に多いですが、それは問題ごとにどうやって場合分けするのかを暗記しようとするから、というのが一因です。

場合分けの仕方はいくらでもパターンを作れてしまうので、是非手を動かして実験することを心掛けてみてください。

ちなみに今回は区間が動くパターンの中でも「区間の幅は固定されていて、区間の位置が変わる」というものを紹介しました。

もちろん場合によっては「区間の端が片方だけ固定されていて、もう片方が動く」などのパターンも考えられます。

これでもやることはいつも通りで、「動かないものを図示して、動くものを実際に動かしてみることで場合分けの仕方を決める。」これに尽きます。

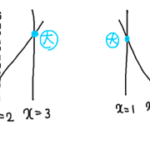
例えば先ほどの例題がｙ＝ｘ^２＋４ｘ＋８（２≦ｘ≦ａ）  のようになっていたら、最初に書く図は二次関数のグラフとｘ＝２ という区間の（動かないほうの）端です。

後はｘ＝２ より右側でａを動かして最大値、最小値がどう変化するかを考えるということです。（ちなみにちょっと実験するとこの問題は場合分けがいらないことに気付きます。）

******************************
全国対応！高校数学・物理化学専門の
オンライン家庭教師・個別指導学習塾、
栃木県宇都宮市近辺の家庭教師を
お探しならこちらをクリック
↓　↓　↓