【数学1】図形と計量（三角比）④／180°ーθ、90°ーθ、90°＋θの三角比

【数学1】図形と計量（三角比）③／三角比の拡張（90°≦θ≦180°の場合）　からの続き

単位円と角度

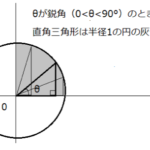
単位円周上にある角度θの直角三角形の頂点Pが単位円周上を動く場合、θが0°、90°、180°のときにはsinθ、cosθ、tanθはどうなるでしょうか？

下の図を見ながら考えてみましょう。
座標で考えるのがポイントです。

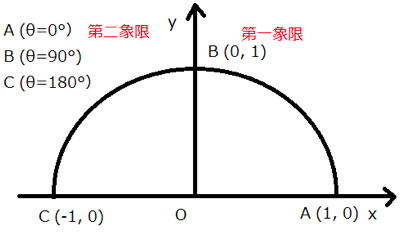
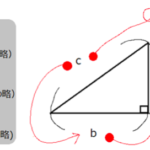
xy座標上のA、B、Cの位置から考えれば分かります。

・θ=0°の場合
座標はA（1,0）なので
sinθ＝０、cosθ＝１、tanθ＝０

・θ=90°の場合
座標はB（0,1）なので
sinθ＝１、cosθ＝０
tanθは存在しない

・θ=180°の場合
座標はB（ー1,0）なので
sinθ＝０、cosθ＝ー１、tanθ＝０

なお、ここでθ=90°のときにtanθが存在しないのは、分母がゼロになる数は存在しないからです。

これにより、θが第1象限と第2象限にある単位円周上を動くとき（ 0°≦θ≦180）、sinθ、cosθ、tanθの範囲は以下のようになることがわかります。
・０≦sinθ≦１
・−１≦cosθ≦１
・tanθは任意の実数値を取る
（ただしθ≠９０° ）

180°ーθ（補角）の三角比

単位円周上にx軸の正の向きとなす角度が鈍角θの点P（ーx,y）を取ると、以下のように補角は180°-θとなります。

今回はこの補角に注目します。

（なおxの値にマイナスが付けているのは、θが鈍角の時に点Pは第二象限になりxの値は必ずマイナスになるため、分かりやすいようにマイナスを付けました）

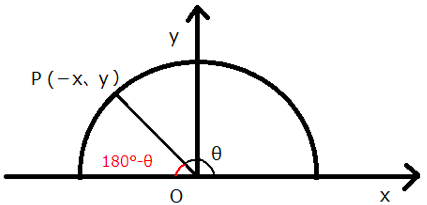
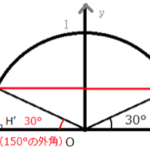
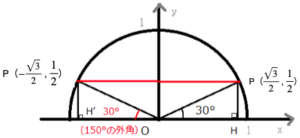
ここで補角（180°ーθ）の三角比を求めるために、下図のようにPからx軸に垂線を下した直角三角形⊿OPHと、その三角形をy軸について対称移動させた⊿OP’H’を作ります。

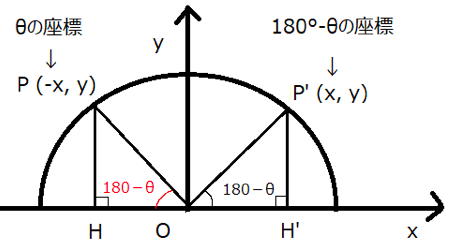
P（ーx,y）は鈍角θが、P’（x,y）は(180°-θ)が単位円周上にとる座標になります。

両方の座標が単位円上に取る座標が分かったので、それぞれの三角比を求めると次の表のようになります。

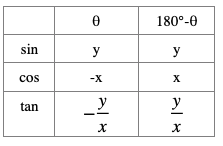
図を見て直感的にも分かりますが、表から三角比の絶対値は全部同じで、cosとtanの符号だけが異なることが分かります。

cosとtanの符号が変わるのは、180°-θが第二象限にあるからです。

そしてこれを式で表すと次のようになります。

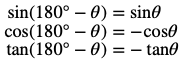
この3つの式が
180°-θ（補角）の公式です。

暗記ではなく図から理解するようにしましょう。

90°＋θの三角比

次にθが鋭角のときの三角比と、θ＋90°の鈍角の三角比の関係はどうなるのか考えてみましょう。

ここでも単位円の図を描いて考えてみます。

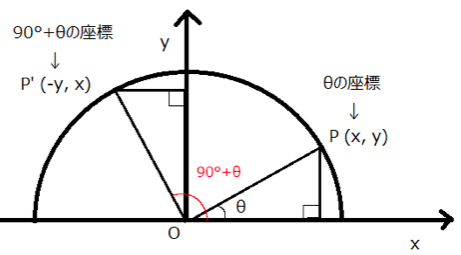
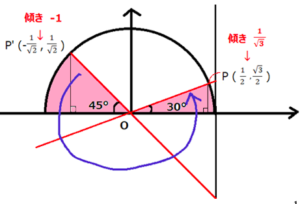
P（ｘ,ｙ）は鋭角θが、
P’（ーy,ｘ）は(90°+θ)が
単位円周上にとる座標になります。

上の図から分かるように
P（ｘ,ｙ）のxの値が
P’（ーy,ｘ）のyの値に、
P（ｘ,ｙ）のyの値が
P’（ーy,ｘ）のxの値に
なっていることに注目してください。

両方の座標が単位円上にとる座標が分かったので、それぞれの三角比を求めると下の表のようになります。

これも図を見て直感的に分かると思いますが、表から一方がsinならcos、cosならsinになり、tanは逆数になることが分かります。

また180°-θと同様に、第2象限にある座標のcosとtanにはマイナスがついていることが分かります。これを式にすると以下のようになります。

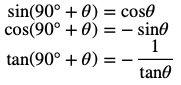
この3つの式が90°+θの公式です。

180°-θより少し複雑になりましたが、ポイントはsinならcosに、cosならsinに、tanは逆数になるところです。

そしてここでもcosとtanの符号が変わってくることも忘れないようにしましょう。

これも公式ではなく、図形で理解して覚えましょう。

90°-θの三角比

最後に90°-θの場合です。

これも図形から考えてみましょう。

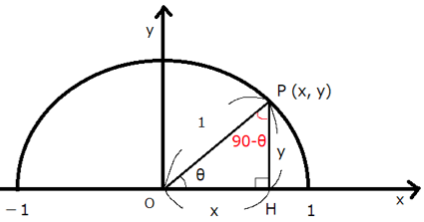
単位円周上にxの正の方向となす角度が鋭角θになる点P（ｘ,ｙ） を取り、Pから垂線を下してx軸と交わる点をHとします。

すると ⊿OPHの∠OPHは90°-θとなります。

ここでこの三角形の向きを変えて配置します。

⊿OPHと区別するために、∠H’OP’=90°-θとなる点P’を取り⊿OP’H’を作ります。

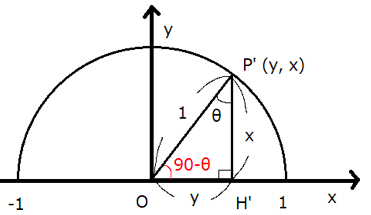
すると上の図のようになるので、座標がθを鋭角とする三角形とはx値とy値の位置が入れ替わることが分かります。

そして単位円周上の座標も分かったので、以下のように三角比を出すことができます。

こちらも90°＋θのように、表から一方がsinならcos、cosならsinになり、tanは逆数になることが分かります。

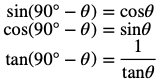
この3つの式が、90°-θの公式です。

今度は90°-θが鋭角で第一象限の角なので、cosもtanも符号が変わることはありません。

他は90°+θと同じです。

まとめ

今回は180°-θ、90°＋θ、90°-θの公式について説明しました。

ここでも大切なのは「座標で考える」ことです。

そして角度が第一象限にあるのか、第二象限にあるのかを必ず確かめるようにしましょう。

そうすれば符号を間違えることもありません。

今日学んだ角度の公式と、三角比の相互関係のときに学んだ公式を組み合わせた問題がよく出題されるので、両方ともしっかり理解しておきましょう。

******************************
全国対応！高校数学・物理化学専門の
オンライン家庭教師・個別指導学習塾、
栃木県宇都宮市近辺の家庭教師を
お探しならこちらをクリック
↓　↓　↓