二次関数のグラフと平方完成、グラフの平行移動が置き換えでできる理由

二次関数は式が与えられたときに正確にグラフの位置、形を読み取る必要があります。

しかし、ｙ＝ａｘ^２＋ｂｘ＋ｃの形のままですぐ分かることは、上に凸なグラフか、下に凸なグラフかということくらいです。

頂点の座標がすぐに分かるわけではありません。

そのためｙ＝ａｘ^２＋ｂｘ＋ｃを変形して、式を一目見ただけで頂点の座標がすぐに分かる形にします。

その時に使う方法が平方完成と呼ばれるものです。

１、平方完成

もっと具体的に言うと、
ｙ＝ａｘ^２＋ｂｘ＋ｃを
ｙ＝ａ（ｘーｐ）^２＋ｑの形に
変形することを平方完成するといいます。

平方完成することによって頂点の座標を知ることができます。

何やら難しそうですが、実質（ｘ＋ａ）^２の展開をすることと変わりません。

試しにいくつか平方完成してみて感覚を掴んでみましょう。

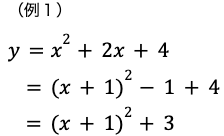
（ｘ＋１）^２は展開すると
ｘ^２＋2ｘ＋1です。

このうち最初の二項は与えられた式にも入っていますね。

しかし1は元の式にはなかったので引き算します。

これで（ｘ＋１）^２ −１の部分だけ見ると与えられた式の最初二項ｘ^２＋2ｘ と同じになりました。

後は定数項4も足して
（ｘ＋１）^２ ＋３ とすると
完全に与えられた式の右辺に一致します。

これで平方完成完了です。

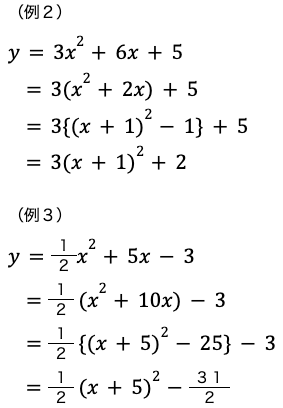
（例２）（例３）は（例１）とほとんどやり方は同じですが、一工夫必要です。

与えられた式のままだと、さっきのようにするのは少し大変です。

違いはなんでしょう。

それは二次の項の係数が1ではないということです。

なので二次の項の係数で括ります。

（例１）を見て分かるように、定数項は後から足せばいいので実質平方完成のメインはｘ^２の項とｘの項です。

なのでここだけ括ります。
そこまでできたら後は同じです。

次に（ｘ＋１）^２ とか（ｘ＋５）^２ とかに変形するのですが、これは１とか５のところに一次の係数の半分を書くだけで大丈夫です。

なぜかというと、

のように、展開すると一次の項は2倍されるからです。

2倍してもとに戻ってほしいなら、最初に半分にしておけばいいということです。

言い替えると平方完成は

の定数項ａ^２を左辺に移項した

を行っているだけです。

２、二次関数のグラフ

それではこの平方完成を用いて二次関数のグラフを書いてみましょう。

まずは中学校の時に学習済みの
ｙ＝ａｘ^２ のグラフを思い出してみましょう。

これは原点を頂点とする放物線でした。
ａ＞0 なら下に凸、ａ＜０なら上に凸ですね。

平方完成と二次関数のグラフ

さて次にｙ＝ａｘ^２の式で
ｙをｙーｑに、ｘをｘーｐに
置き換えてみます。

すると
  ｙーｑ＝ａ（ｘーｐ）^２
∴ｙ＝ａ（ｘーｐ）^２＋ｑ

と先ほどの平方完成で目指していた形になりました。

この置き換えが図形的に何を意味しているかは、一通り話が済んでから説明します。

今この段階ではｙ＝ａｘ^２のグラフをｘ軸の正の方向にp、ｙ軸の正の方向にqだけ平行移動させたという事実だけを
知っておいてください。

つまり、この平行移動によって
頂点は点（ｐ、ｑ）という点に移ります。

要はｙ＝ａ（ｘーｐ）^２＋ｑ の形にすると、点（ｐ、ｑ）という点が頂点で、軸がｘ＝ｐ だということがわかります。

これが平方完成の目的です。

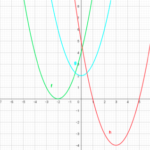
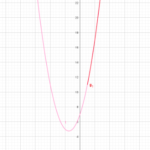
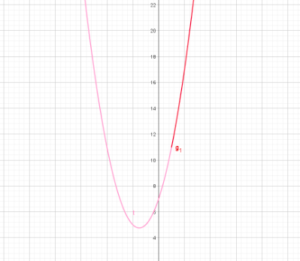
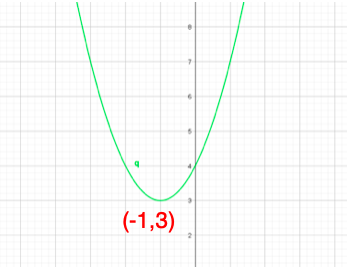
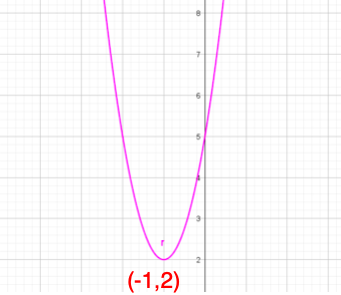
では先程の例題のグラフを書いてみます。

もう平方完成は終わっているので、そこから軸、頂点の座標を読み取るだけです。

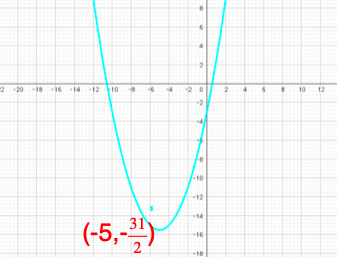
手書きで書くときは頂点の座標、y軸、x軸とグラフの交点だけは取って、それ以外の点は書かなくても大丈夫です。

二次関数のグラフの平行移動

最後に先ほど出てきた置き換えが、平行移動になる理由を説明します。

ｙ＝ｆ（ｘ）という関数をx軸方向にp、y軸方向にq平行移動してｙ＝ｇ（ｘ）という関数にすることを考えてみます。

直線だろうが曲線だろうが座標平面上の図形は全て点の集合です。

よって平行移動は１つの点で平行移動を考えればよいです。

ｙ＝ｆ（ｘ） を平行移動すると、
もともとｙ＝ｆ（ｘ）上にいた
点（ｘ，ｙ） は（ｘ＋ｐ，ｙ＋ｑ） に
移っているはずです。

そして、この点はｙ＝ｇ（ｘ）上の点でもあるはずです。

ということは（ｘ＋ｐ，ｙ＋ｑ）をｙ＝ｇ（ｘ）に代入すれば、その式は等号が成り立つということになります。

しかし、今回はそのｙ＝ｇ（ｘ）が知りたいので、代入しようがありません。

よって、逆の操作を考えます。

つまり、 ｙ＝ｇ（ｘ）上の点 （ｘ，ｙ）をx軸方向にーp、y軸方向にーqだけ平行移動してみます。

すると、平行移動した点 （ｘーｐ，ｙーｑ）というのはｙ＝ｆ（ｘ）上の点になるはずです。

ｙ＝ｆ（ｘ）はすでに式がわかるグラフですから、ここに（ｘーｐ，ｙーｑ）を代入することはできます。

実際に代入したｙーq＝ｆ（ｘーp）というのが
ｙ＝ｇ（ｘ）が満たさなければいけない式だということが分かりました。

以上をまとめると、グラフをx軸方向にp、y軸方向にq平行移動させるということはｘをｘーｐ、ｙをｙーｑに置き換えてあげればよいということになります。

二次関数の最大値最小値の求め方（定義域がない場合と定義域がある場合）に続く

******************************
全国対応！高校数学・物理化学専門の
オンライン家庭教師・個別指導学習塾、
栃木県宇都宮市近辺の家庭教師を
お探しならこちらをクリック
↓　↓　↓