【数学1】図形と計量②／特別な角度の三角比と三角比の相互関係の使い分け

【数学１】図形と計量①／三角比（sin、cos、tan）と２通りの求め方からの続き

前回は、中学で学んだ数学の復習をしながら三角比 sinθ、cosθ、tanθについて勉強しました。

前回の復習もかねて早速、三角比を使ってみましょう。

１、特別な角度の三角比

sin30° 、cos30° 、tan30°の場合

＜問題1＞
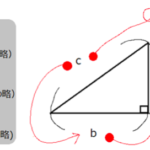
下図の直角三角形ABCにおいて sin30° 、cos30° 、tan30° を求めよ。

---

　

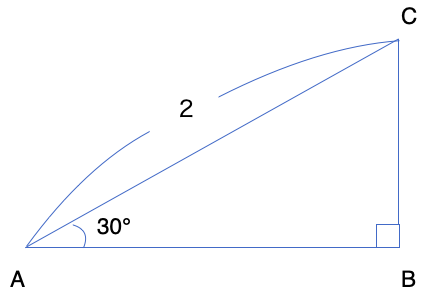
「斜辺の長さしか分からないから無理……」と
一瞬思うかもしれませんが、

中学で学んだことを生かせば、他の辺の長さがわかります。

図のような直角以外の角度が30°、60°の直角三角形の辺の比は下図のようになるのでした。

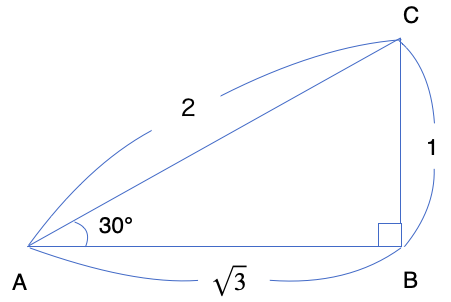
この図からsinθ、cosθ、tanθを求めることができます。

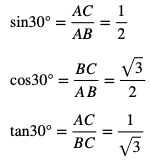
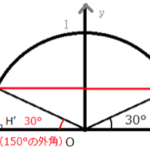
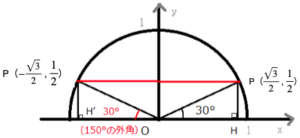
sin60° 、cos60° 、tan60°の場合

＜問題2＞
sin60° 、cos60° 、tan60° を求めよ。

---

先程の図の向きを変えると、下のようになります。

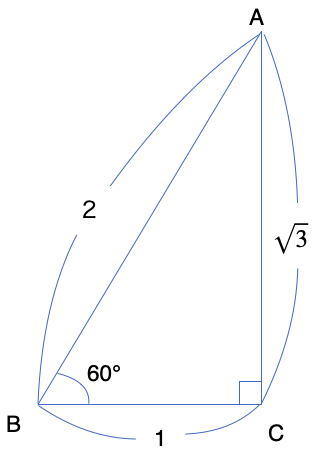
この図から

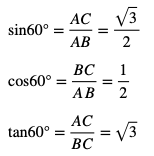
どうでしたか？

30°の直角三角形と同じ手順を踏めば解けるので、簡単だったのではないでしょうか。

次に直角二等辺三角形の三角比を求めて見ましょう。

sin45° 、cos45° 、tan45°の場合（直角二等辺三角形の三角比）

＜問題３＞
sin45° 、cos45° 、tan45° を求めよ。

---

中学で学びましたが、鋭角が45°の直角二等辺三角形の辺の比は下図のようになります。

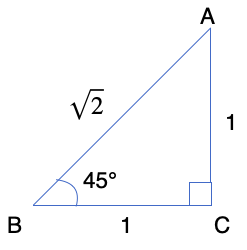
したがって

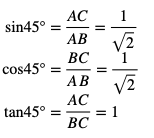
となります。

特別な角度の三角比一覧表

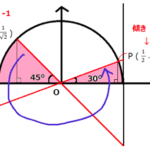
これまで解いてきた鋭角θが30°、45°、60°の直角三角形の三角比を一覧表にすると、以下のようになります。

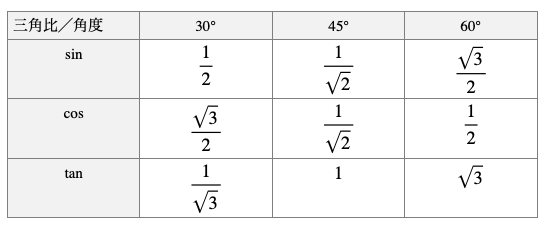
30°、45°、60°の三角比は頻繁に問題に出題されるので、上記の表を暗記するまで頭に叩き込んでください。

このよく問題に出題される角度の三角比は、単に丸暗記するだけでなく、三角比を導くプロセスに目を通しておくことで、万一忘れてしまっても自力で導き出せると思うのでご紹介しました。

２、三角比の相互関係

ここまで三角比sinθ 、cosθ 、tanθ の求め方についてお伝えしてきましたが、ここからは三角比同士の関係について学びましょう。

三角比同士の関係は数式で表すことができます。

まず、三角比同士の関係を表す数式を導くプロセスを見ていきましょう。

三角比の相互関係①

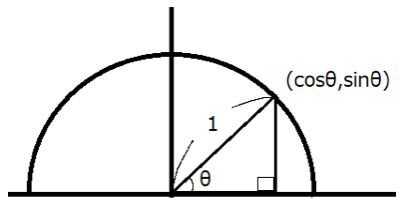
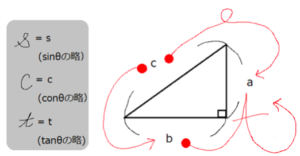
上の直角三角形を見てください。

斜辺が長さ1、
底辺の長さはcosθ、
高さはsinθであることが分かりますね。

この場合、三平方の定理により以下の式が成り立ちます。

ここでちょっと注意して欲しいのが

と書くことです。

だと2乗がθ、つまり角度にかかってしまうので、「2乗はsinだけに掛かっているんですよ」ということを示すためにsinのすぐ後ろ、角度を表すθの前に2乗をつけるという表記を使います。

三角比の相互関係②

次に下図の直角三角形があるとします。

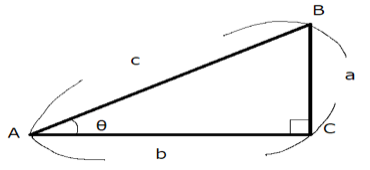
この場合のtanθは以下の式になります。

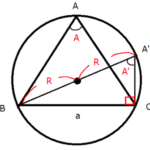
この直角三角形が半径1の円に内接するとします。

するとtanθは、以下のように
sinθとcosθで表すことができます。

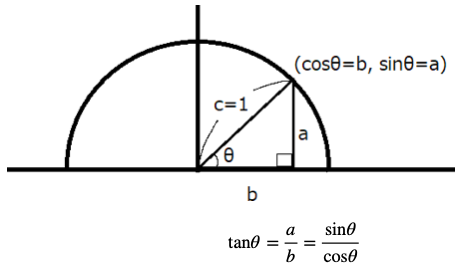
三角比の相互関係③

の両辺をcos^２θで割ってみます。すると

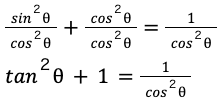
となり、以下の公式が導けます。

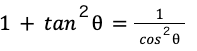
三角比の相互関係まとめ

以上の3つの数式のうち
②と③の分数の分母は0にはならないので、cosθ≠０です。

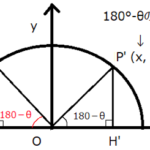
したがって、xy座標軸上で
x＝0になってしまう90°は対象にはなりません。

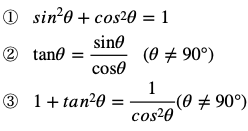
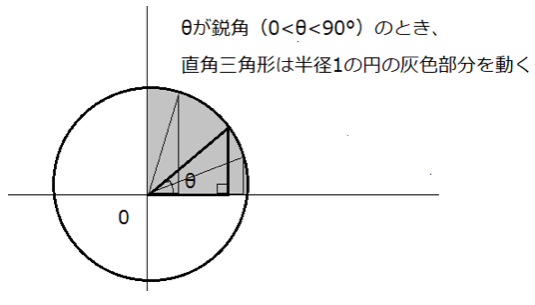
またθが鋭角の場合、直角三角形は以下のように第1象限上（xy座標軸上でxの値もyの値も正の座標）で動き、第1象限上にある辺の長さの比なので、sinθ、cosθ、tanθはすべて正の数になります。

それではこの3つの数式を使って、実際に問題を解いてみましょう。

三角比の相互関係を使う練習問題

---

＜解答＞

まずθが鋭角ということから、
sinθ、cosθ、tanθはすべて正の数になります。

次にsin²θ＋cos²θ＝１ の式を使います。

この問題のようにsinθもしくはcosθの値が与えられているときには、この式を使いましょう。

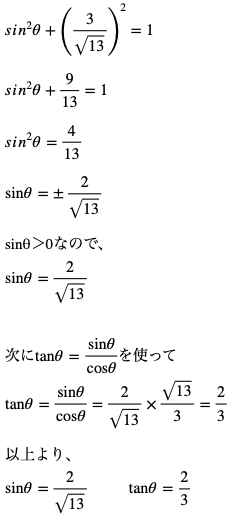
最初にsin²θ＋cos²θ＝１の式により、sinθとcosθのうち与えられていない方の値を出します。

それから

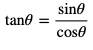
の式から、tanθの値を導き出すという流れです。

それでは今度はtanθの値を与えられている問題はどうでしょうか？

＜問題2＞

---

まずθが鋭角ということから、sinθ、cosθ、tanθはすべて正の数になることを確認します。

そしてこの問題のように、tanθの値が得られているときには、

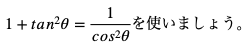
すると、以下のようになります。

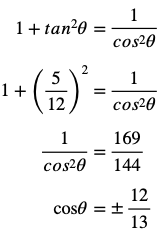
θは鋭角なので、cosθ>0になり

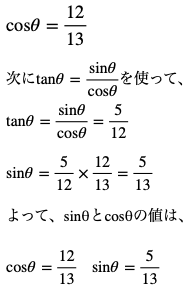
いかがでしたか？

tanθが与えられている時には、

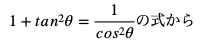
cosθの値を出して、その後に

sinθの値を導き出すという流れです。

与えられている三角比の値によって、使う式はどれになるのかをしっかり頭に入れてくださいね。

今日出てきた数式は三角比の中でも特に重要な数式です。

ですので数式が成立するまでのプロセスにしっかり目を通して、忘れてしまっても自力で導き出せるようにしておきましょう。

******************************
全国対応！高校数学・物理化学専門の
オンライン家庭教師・個別指導学習塾、
栃木県宇都宮市近辺の家庭教師を
お探しならこちらをクリック
↓　↓　↓