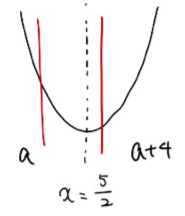
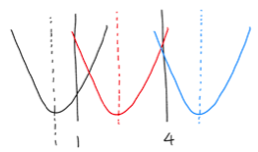
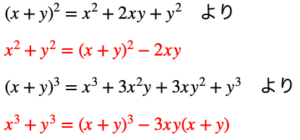二次関数の最大値・最小値/関数が固定されて区間(定義域)が動く場合
二次関数の最大値・最小値/区間(定義域)が固定されて軸が動く場合 からの続き 今回は関数が固定されて区間が動く場合の二次関数の最大値・最小値の求め方について説明します。 区間(定義域)が固定されて関数の軸が動く場合と並ん […]
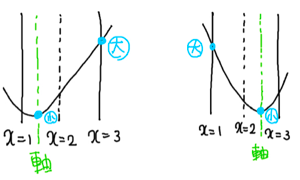
二次関数の最大値・最小値/区間(定義域)が固定されて軸が動く場合
文字を含む二次関数の最大値・最小値の求め方(グラフによる場合分け)からの続き 二次関数の最大値・最小値を求める問題で最も重要なのは「定義域や関数が動くときの最大値・最小値」を求める問題です。 この問題は丸暗 […]
文字を含む二次関数の最大値・最小値の求め方(グラフによる場合分け)
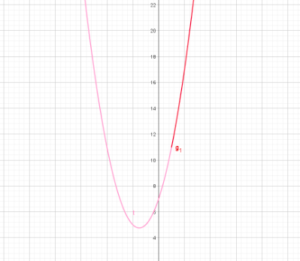
二次関数の最大値・最小値を求めるうえで、毎回必ず全ての係数が分かっているとは限りません。 ここではそのような二次関数の最大値・最小値の求め方について見ていきます。 必要な知識は平方完成くらいですので早速例題を通して見てい […]
二次関数の最大値最小値の求め方(定義域がない場合と定義域がある場合)
二次関数のグラフと平方完成、グラフの平行移動が置き換えでできる理由からの続き 二次関数では最大値と最小値を求めることをよく行います。(数IIや数IIIへ学習を進めると三次関数や四次関数などの一般の曲線でも行います) 二次 […]
二次関数のグラフと平方完成、グラフの平行移動が置き換えでできる理由
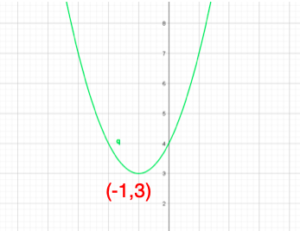
二次関数は式が与えられたときに正確にグラフの位置、形を読み取る必要があります。 しかし、y=ax2+bx+cの形のままですぐ分かることは、上に凸なグラフか、下に凸なグラフかということくらいです。 頂点の座標がすぐに分かる […]
【数学Ⅰ】分母の有理化、基本対称式から対称式の値を求める方法
中学でやった分母の有理化の発展版を 高校入学後学びますが、 そこは比較的簡単だと思います。 しかし、その分母の有理化の 応用問題で登場する対称式については よく理解できないこともあるのではないでしょうか? そこでここでは […]
【数学Ⅰ】たすき掛けによる因数分解〜組み合わせを楽にみつける方法
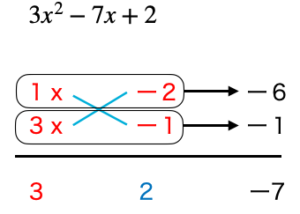
高校でまず新たに学ぶことと言えば たすき掛けによる因数分解があります。 その組み合わせを見つけるのも 最初は苦労するでしょう。 「慣れればすぐ見つかるようになる」 と、学校の先生は言うかもしれません。 です […]