【数学1】図形と計量(三角比)③/三角比の拡張(90°≦θ≦180°の場合)


【数学1】図形と計量②/特別な角度の三角比と三角比の相互関係の使い分け からの続き
三角比の拡張
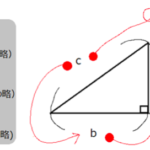
ここまで三角比sinθ、cosθ、tanθでは、直角三角形の角度θは90度より小さい角度「鋭角」の場合について考えてきました。
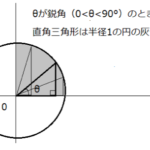
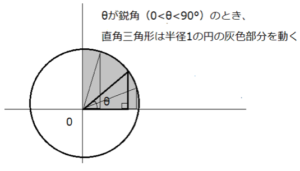
例えば下図のように半径rの円周上にA (r,0)を取り、∠AOPが鋭角(0°<θ<90°)となるようなP(x,y)を同じく半径rの円周上に取るとします。
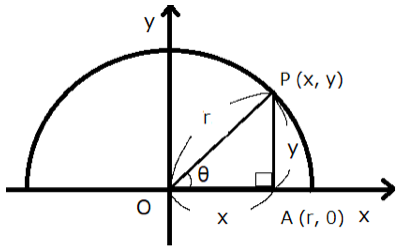
この場合sinθ、cosθ、tanθはどうなるでしょうか?
斜辺が円の半径r、底辺がx、高さがyの直角三角形なのでsinθ、cosθ、tanθを導く式は、以下になります。
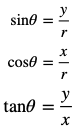
ここで円の半径rをr=1にしてみましょう。
するとはsinθ、cosθ、tanθは次のようになります。
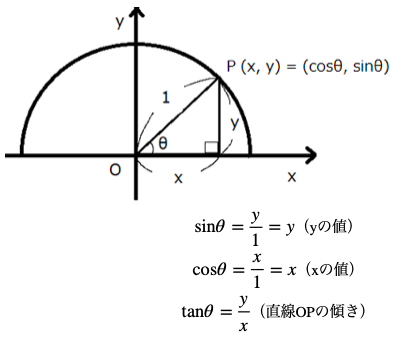
半径1の円周上にある
点 P(x,y)=(cosθ,sinθ)となり
tanθは直角三角形の斜辺OPの傾きと等しいことが分かります。
ここから分かることはx,y軸上にある半径1の円周上にある座標が分かれば、そこからsinθ、cosθ、tanθの値が分かるということです。
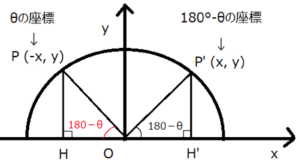
これを踏まえた上で、下図のように角度θが直角90°を超える鈍角の場合を考えましょう。
(90°≦θ≦180°)
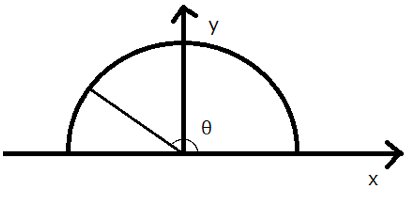
θが鈍角の場合には直角三角形はできないので、三角比を考える時は座標で考えます。
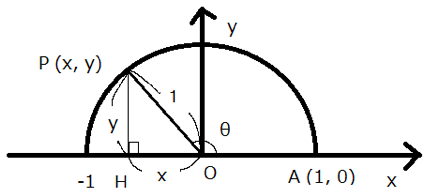
上図のように半径1の円周上にA (1,0)と∠AOP=θ(鈍角)となる点P(x,y)を取ります。
ここに座標を用いて三角比を求める方法を当てはめると次のようになります。
このように鋭角でも鈍角でも座標だけを考えれば、三角比は簡単に導き出せることができます。
(ちなみに今まで何度も登場したこの半径1の円のことを「単位円」と言います。)
鈍角θの場合の三角比を求める
それでは鈍角θの場合の三角比を実際に求めてみましょう。
まずはθ=150°の場合です。
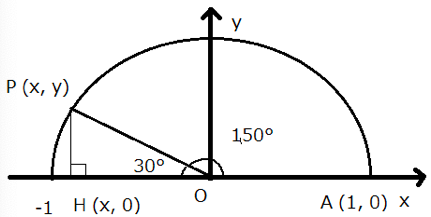
単位円の円周上にA (1,0)と∠AOP=150°になる点P(x,y)を取り、P(x,y)からx軸に下した垂線とx軸が交わる点をH(x,0)とします。
ここでxとyの値を求めましょう。
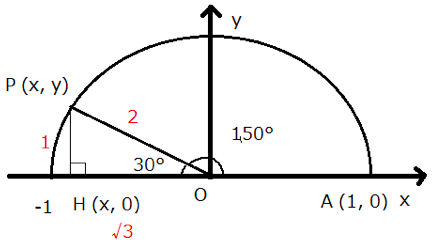
△OPHは鋭角30°の直角三角形になります。
上図では赤い数字が鋭角30°の直角三角形の辺の比を示しています。
(ちなみに∠POHの角度30°は「(150°の)補角」と言います。)
OPは円の半径は1なので
これを辺の比に当てはめると
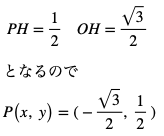
になります。
点P(x,y)のxの値がマイナスになることに注意しましょう。
点P(x,y)は第二象限、つまりx軸はマイナス、y軸はプラスの範囲にあるので、xの値は常にマイナスになります。
以上より単位円の円周上にある∠AOP=150°となる場合
![]()
θ=150°の三角比は次のように求めることができます。
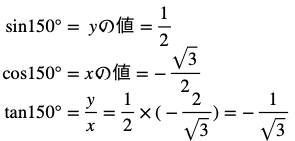
三角比の拡張と鋭角の三角比
ここまでの説明でお気付きかもしれませんが、実は鈍角θの三角比と補角(180-θ)の直角三角形の三角比は鏡合わせなのです。
θ=150°の図を使って、実際に見てみましょう。
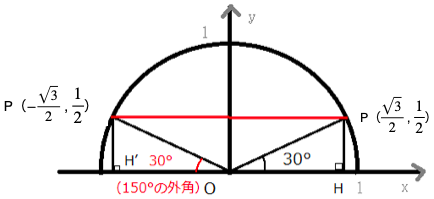
sinθ=yの値なので、
高さが同じため同じ値です。
cosθ=xの値なので、
絶対値は同じで正負の符号のみ違います。
tanθ=y/xなので、
絶対値は同じで正負の符号のみ違います。
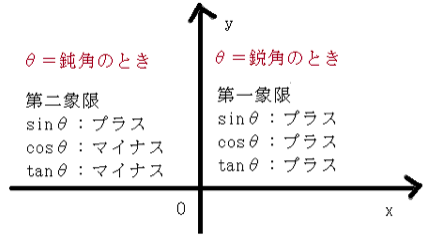
符号に関しては、xy座標軸を見れば一目瞭然です。
頭の中にxy座標を思い浮かべれば、符号を間違えることはないでしょう。
拡張された三角比を含む特別な角度の三角比
最後に鈍角θの重要な角度の三角比をご紹介します。
鈍角θの補角となる鋭角との関係をしっかりチェックして符号を間違えないようにしましょう。
丸暗記ではなく図を見てしっかり理解することが大切です。
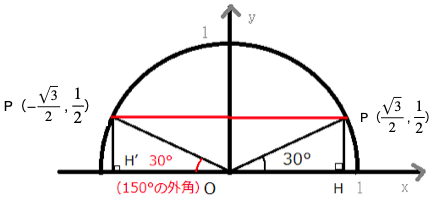
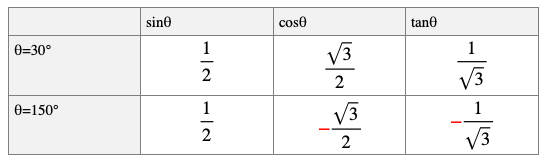
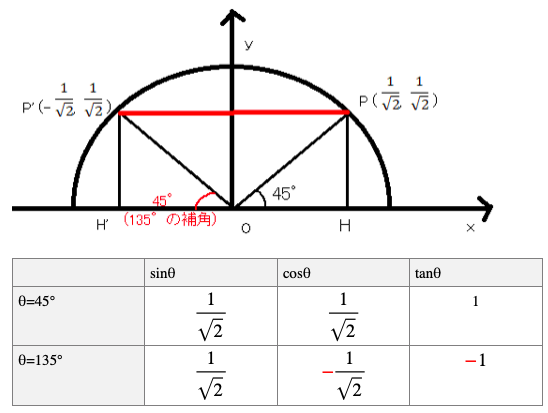
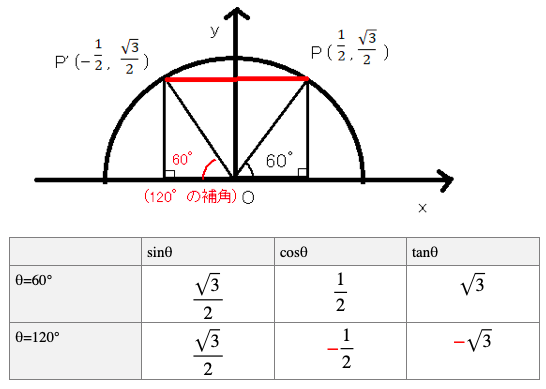
鋭角=鈍角の補角の場合は、このようにsinθ、cosθ、tanθの絶対値は同じで、 cosθ、tanθは符号が異なることに注意しましょう。
最後に
今回は三角比の拡張について説明してきました。
大切なのは「座標で考える」ことです。
鋭角の場合のように角度θの三角形にこだわらずに「座標」と「補角をもつ直角三角形」に目を向けるよう意識しましょう。
******************************
全国対応!高校数学・物理化学専門の
オンライン家庭教師・個別指導学習塾、
栃木県宇都宮市近辺の家庭教師を
お探しならこちらをクリック
↓ ↓ ↓