二次不等式の図による解き方/絶対値が付く二次関数のグラフの書き方


二次方程式解き方と解の公式、判別式と二次関数の共有点の個数の関係 からの続き
二次不等式とは、多項式の最も大きい次数が二次式になっている不等式です。
例えばx2+x+1≦0というのは二次不等式です。
ax2+bx+c≦0はa=0の時は一次不等式、aがそれ以外の実数の時は二次不等式になります。
二次不等式の考え方
二次不等式は1つ1つの出題パターンを覚えようとすると、種類がたくさんあるので大変ですが、すべてに共通するたった1つのことさえ覚えておけば、どんなパターンが来ても基本的に解けます。
そのたった1つのことというのは「二次不等式は図で考える」ということです。
数学では図で考えると、簡単になることが多いです。
二次不等式もその一つで、図なしで解くのは不可能と言っても過言ではないくらいに図が大切です。
図の大切さを少し知ってもらったところで実際にいくつかの例題を通して基本的な二次不等式の解き方を掴んでいきましょう。
二次不等式の基本問題
例題:次の不等式を解け
①x2+3x+2<0
②x2≦9
③ーx2+6x−5>0
(解答)①
不等号( ≦、≧、<、>)を等号(=)に置き換えてみると二次方程式の形になっています。
ですので二次不等式では二次関数のグラフを使って図形的に解いていきます。
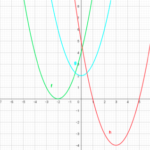
①左辺=(x+1)(x+2)<0
これは二次関数
y=(x+1)(x+2) の
y座標が0になる部分だから
図の色が付いた部分
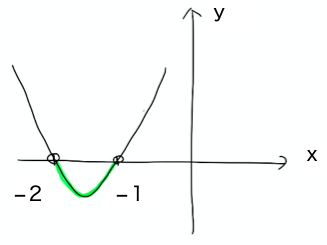
よって求める範囲は
−2<x<−1
解答②
右辺を移項して
x2ー9≦0
①と同様にすると
(x−3)(x+3)≦0 なので
求める範囲は図の色付き部分
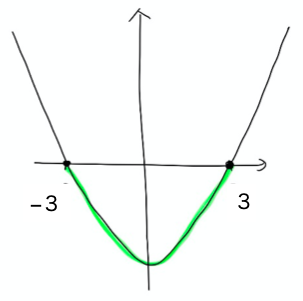
よって−3≦x≦3 が求める範囲
解答③
左辺=ー(x−5)(x−1)>0
①と同様に図を書くと
求める範囲は色付きの部分で
1<x<5
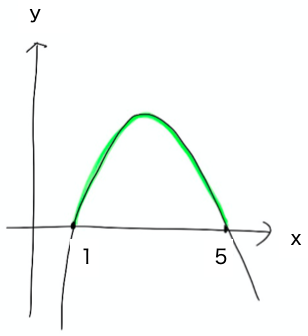
以上を簡単にまとめると、二次不等式の幾何的意味(見た目で分かる意味)は
・(二次式)< 0 ならy = (二次式)のグラフがx軸よりも下にある範囲
・(二次式)> 0 ならy = (二次式)のグラフがx軸よりも上にある範囲
ということになります。(≦、≧ はx軸も含む)
二次不等式の応用問題
ここまでのことを踏まえて、少し応用的な問題も解いてみましょう。
問題:次の二次不等式を解け。
①ー2x2+4x−3<0
②|x2−2x|≦1
(解答)先程の問題と比べると難易度が上がりましたが、グラフを書けば同じように解くことができます。
(1)まず二次の係数がマイナスだと解きづらいので両辺にマイナスを掛けます。
(与式)↔ 2x2ー4x+3>0…①
左辺のグラフを書くと図のようになります。
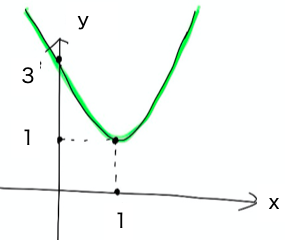
よってこの不等式①を満たすのは「全ての実数」です。
(2) 左辺のグラフを書くと図のようになります。
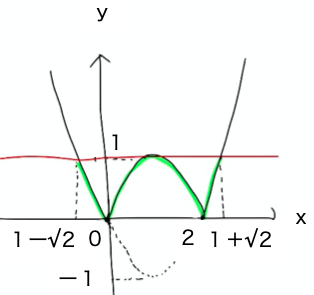
これが1以下になる範囲の図の色付き部分が不等式を満たすので、答えは
1ー√2≦x≦1+ √2
この問題はどちらも少し難しく、かつ重要なので少しだけ補足をしておきます。
(1)の問題で与えられた式の不等号が逆、すなわち
ー2x2+4x−3>0
の場合はどうなるでしょう。
先ほどと同じように解いてみると、この不等式を満たすxは見つからないことが分かります。
この場合は「解なし」と答えておけば大丈夫です。
絶対値が付く二次関数のグラフ
次は(2)です。
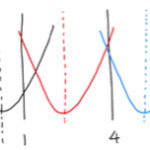
まずは絶対値付き関数のグラフの書き方ですが、次の手順で描くことができます。
①絶対値が付いていない状態のグラフを書く
②x軸より下、つまりy座標が負の部分をx軸について対称に折り返す。
これでグラフが書けたら後はいつも通りです。
グラフを使わない二次不等式の解き方
また、(2)には別解があるので、ご紹介します。
(2)(別解)
|x2−2x|≦1より
ー1≦x2−2x≦1
中辺を平方完成して、整理すると
0≦(x−1)2≦2
xが実数なので
0≦(x−1)2は明らかに成り立つので
(x−1)2≦2を求めれば良い。
両辺の平方根を取ると
ー√2≦x−1≦√2
両辺に1を足して
1ー√2≦x≦1+ √2
このように図なしでも解くことは可能です。
ただ見て分かるように不等式で平方根を取ったり絶対値を外したりするので、ある程度計算に慣れていないと難しいかもしれません。
******************************
全国対応!高校数学・物理化学専門の
オンライン家庭教師・個別指導学習塾、
栃木県宇都宮市近辺の家庭教師を
お探しならこちらをクリック
↓ ↓ ↓