【数学1】図形と計量(三角比)⑤三角方程式、三角不等式の解き方


【数学1】図形と計量(三角比)④/180°ーθ、90°ーθ、90°+θの三角比 からの続き
三角方程式
sinθ、cosθ、tanθのθという未知の角度の三角比を含む方程式のことを三角方程式と言います。
このとき未知の角度θが何度かを求めることを「三角方程式を解く」といいます。
実際に問題を見てみて説明していきます。
三角方程式①
以下の三角方程式の問題を解いてみましょう。
<問題①>
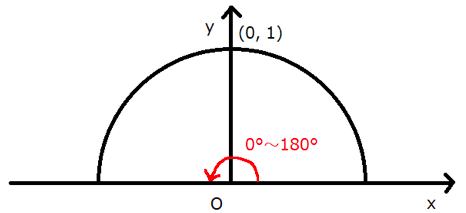
0°≦θ≦180°のとき、次の三角方程式を解け。
$$\sqrt{2}cosθ+1=0$$
$$cosθ=-\dfrac{1}{\sqrt{2}}$$
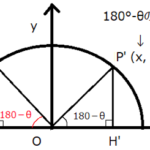
この条件を満たすcosθは、下図の単位円周上の点Pの$x$座標になります。
符号がマイナスなので、θは鈍角であることも分かります。
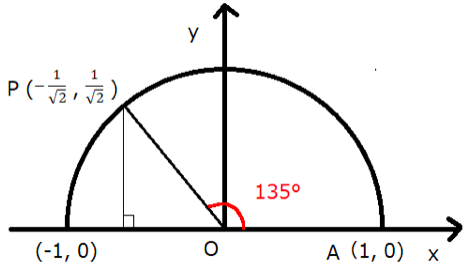
点$A(1,0)$ を取ると、$\angle AOP =θ$なので、$\angle AOP =θ=135^{ \circ }$になります。
よって答えは$135^{ \circ }$になります。
ここでも単位円上の座標の位置を確かめることが大事になってきます。
三角方程式②
sin2θのような三角比を2乗したものが公式に混ざっていても、単位円上の座標の位置からθを求めるのは同じです。
こちらも実際にやってみましょう。
<問題②>
0°≦θ≦180°のとき、三角方程式
$$\sqrt{2}\cos^2 \theta+(3\sqrt{2}+1)\sin \theta-3-\sqrt{2}=0$$
を解け。
まずは$\sin^2 \theta+\cos^2 \theta=1$の公式を使って、$\sin \theta$のみの式にしてみましょう。
$$\sqrt{2}(1-\sin^2 \theta)+(3\sqrt{2}+1)\sin \theta-3-\sqrt{2}=0$$ $$\sqrt{2}-\sqrt{2}\sin^2 \theta+(3\sqrt{2}+1)\sin \theta-3-\sqrt{2}=0$$ $$\sqrt{2}\sin^2 \theta-(3\sqrt{2}+1)\sin \theta+3=0$$
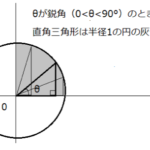
ここで$\sin \theta=t$とすると、$ 0^{ \circ }\leqq \theta \leqq 180^{ \circ } $より$\sin \theta$は下の単位円周上の$y$座標なので、$ 0 \leqq t \leqq 1 $になります。
したがって$$\sqrt{2}t^2-(3\sqrt{2}+1)t+3=0 $$ $$(t-3)(\sqrt{2}t-1)=0 $$ $$t=3,\dfrac{1}{\sqrt{2}}$$ $$0 \leqq t \leqq 1より、t= \sin \theta = \dfrac{1}{\sqrt{2}}$$ $$よって\theta =45^{ \circ },135^{ \circ }$$
下の図のように、図で描いてみると符号や該当する角度がわかりやすいでしょう。
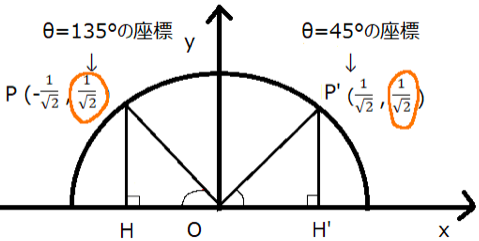
三角不等式
三角比を使った方程式と同じように、未知の角θを含む三角比を使った不等式も解くことができます。
解き方は方程式と似てますが、 sinθ、cosθ、tanθといった三角比の取りうる値の範囲を常に意識するようにしましょう。
<問題③>
0°≦θ≦180°のとき、三角不等式$$\sqrt{3}\tan^2 \theta-(1-\sqrt{3})\tan \theta-1 \leqq 0$$を解け。
ここで$\tan \theta =t$ とすると$$\sqrt{3}t^2-(1-\sqrt{3})t-1 \leqq 0$$ $$(t+1)(\sqrt{3}t-1) \leqq 0$$ $$-1 \leqq t \leqq \dfrac{1}{\sqrt{3}}$$
$\tan \theta$は下図の単位円周上の原点Oと点Pを結ぶ直線の傾きです。
傾き$\dfrac{\sin \theta}{\cos \theta}$ は、$0^{ \circ } \leqq \theta \leqq 180^{ \circ }$の範囲で分母の$\cos \theta =0 $になってしまうθ=90°を除くすべての実数値をとります。
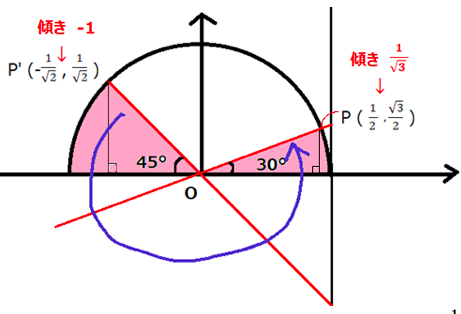
$\tan \theta =t$が$-1 \leqq t \leqq \dfrac{1}{\sqrt{3}}$を取るときには、座標は青い矢印の方向に点P’から点Pまで移動します。
しかし$0^{ \circ } \leqq \theta \leqq 180^{ \circ }$なので、第一象限と第二象限のみが座標の動く範囲となります。
そのため円の下半分は動く範囲とはならず、180°から360°までは対象外です。
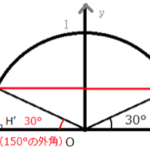
この図ではピンク色の部分の円周上が対象になります。
座標P’はθ=135°(補角45°)なので、答は$$0^{ \circ } \leqq \theta \leqq 30^{ \circ }、135^{ \circ } \leqq \theta \leqq 180^{ \circ }$$となります。
まとめ
三角不等式でも「単位円周上の座標を考える」「三角比のとりうる角度の範囲を考える」という点で三角方程式と基本は同じです。
三角方程式でも三角不等式でも図を描いて基本を押さえて考えていけば必ず解けます。
******************************
全国対応!高校数学・物理化学専門の
オンライン家庭教師・個別指導学習塾、
栃木県宇都宮市近辺の家庭教師を
お探しならこちらをクリック
↓ ↓ ↓