【数学1】図形と計量(三角比)⑥正弦定理とは?その導き方と使い方


【数学1】図形と計量(三角比)⑤三角方程式、三角不等式の解き方 からの続き
ここでは正弦定理についてお伝えします。
正弦定理の「正弦」とは、三角比のsinのことです。
他の三角比であるcosは「余弦」、tan は「正接」です。
今回は「正弦」=sin を使って「外接円と三角形」の関係についての関係式「正弦定理」についてご紹介します。
正弦定理とその導き方
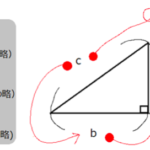
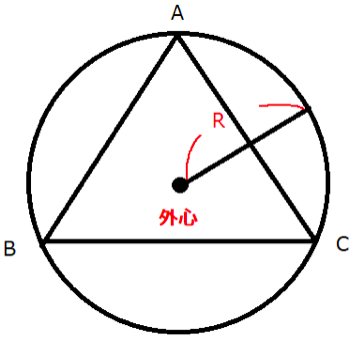
以下のような三角形ABCがあるとします。
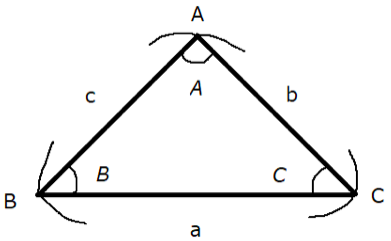
頂点Aの内角$\angle BAC$をA、頂点Bの内角$\angle CBA$をB、頂点Cの内角$\angle ACB$をCとして、その対辺をそれぞれa、b、cとします。
三角比の問題ではこのような表記のされ方が多いので、慣れておきましょう。
次に各頂点を通る円を描きます。
このような三角形の3つの頂点を通る円のことを「外接円」、その中心を「外心」と言います。
この時、外接円の半径をRとすると直径は2Rとなります。
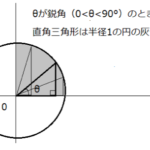
Aが鋭角のとき、下図のように三角形ABCとその各頂点を通る外接円があるとします。
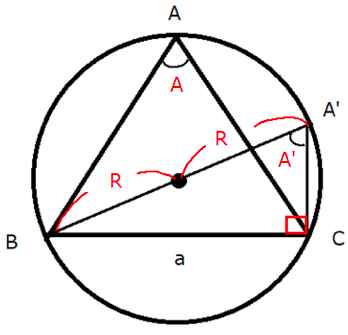
このときAは弧BCの円周角と言えます。
円周角の定理により、同じ弧BCに対する円周角は等しいため、外接円上に線分A’Bが直径と重なるように新たに頂点A’をとると、$\angle A=\angle A’$となります。
以下、Aと同様、頂点A’の内角もA’と表します。
また直径に対する円周角は直角なので、$\angle A’CB=90^{ \circ }$となります。
そのため三角形A’CBは直角三角形になります。
直角三角形A’CBにおいて、sinA’について考えるとき、斜辺は直径の2R、高さはaとなります。
そのためsinA’は、以下の式になります。
$\sin A’=\dfrac{a}{2R}$
さらにA’は弧BCの円周角なのでAと等しいため、以下の式になります。
$\sin A=\dfrac{a}{2R}$
これは、B、Cでも同じことが言えるので
$\sin B=\dfrac{b}{2R}$
$\sin C=\dfrac{c}{2R}$
以上より、以下の公式を導くことができます。
$\dfrac{a}{\sin A}=\dfrac{b}{\sin B}=\dfrac{c}{\sin C}=2R$
これを正弦定理と言います。
正弦定理を使う際には、辺の長さとの部分を使う場合と、半径Rとの部分を使う2パターンがあります。
正弦定理の問題を解く際には、何が問われているのかを明確にして、正弦定理の公式のどの部分を使ったら良いのかを考えましょう。
正弦定理の使い方
それでは正弦定理の具体的な使い方をご紹介します。
三角形の1辺の長さと2つの角度が分かっているときに残りの辺の長さを求める問題は、下の図の正弦定理のうち赤い部分の式で必要な部分を使います。
もう1つは外接円の半径を求める問題です。
外接円の半径を求めるときには、下の図の正弦定理のうち青い部分の式で必要な部分を使います。
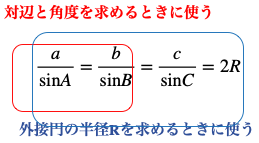
また上の図の正弦定理を
$a=2R\sin A$、$b=2R\sin B$、$c=2R\sin C$
という形に変形して使いやすくしたり
$a:b:c=\sin a:\sin b:\sin c$のように比の形にして使いやすくするという方法もあります。
実際に例題を正弦定理で解いてみましょう。
<例題>
三角形ABCとその外接円において、$B=120^{ \circ }$、$C=15^{ \circ }$、$a=5\sqrt{2}$のとき、外接円の半径RとBの対辺bを求めよ。
<解答>
問題文を図にすると下図のようになります。
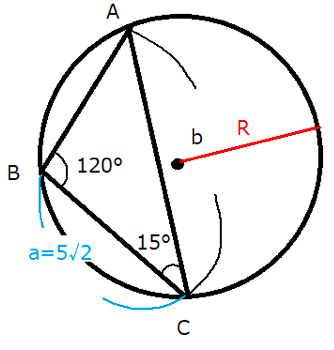
三角形ABCのうちBとCの2つの角度が分かっているので、まずは残りのAを求めます。
三角形の内角の和は180°なので、
$180^{ \circ }-(120^{ \circ }+15^{ \circ })=45^{ \circ }$
Aが45°であることが分かったので、正弦定理を使います。
求めたい値がBの対辺bであり
$\sin A=\sin 45^{ \circ }$の値もわかるので
$\dfrac{a}{\sin A}=\dfrac{b}{\sin B}$
を使います。
わかっている値を代入すると以下のようになります。
$\dfrac{5\sqrt{2}}{\sin 45^{ \circ }}=\dfrac{b}{\sin 120^{ \circ }}$
$∴b=5\sqrt{3}$
次に外接円の半径Rは
$\dfrac{a}{\sin A}=2R$
使って求めることができます。
わかっている値を代入すると以下のようになります。
$\dfrac{5\sqrt{2}}{\sin 45^{ \circ }}=2R$
$∴R=5$
このように「正弦定理」は、三角形のsinの値や関連する辺の長さ、外接円の半径を求めるのにとても便利な公式です。
問題を解くときには、図を描いてみて、その時点で何の値がわかっているのか、何の値が求められているのかを確認してから、公式のどの部分を使うのかを考えましょう。
公式を求める過程をご紹介したので、プロセスも押さえておけば公式を忘れてしまっても自分で導き出せます。
次回ご紹介する余弦定理とともに重要な公式ですので、しっかりと覚えて使えるようにしましょう。