【数学1】図形と計量（三角比）⑦余弦定理とは？その証明と２パターンの使い分け

【数学1】図形と計量（三角比）⑥正弦定理とは？その導き方と使い方 からの続き

今回は余弦定理についての解説です。

余弦定理の「余弦」とは、三角比のcosのことです。

前回の正弦定理ではsinを使いましたが、余弦定理ではcosを使います。

今回はこの「余弦」＝cosを使って「三角形の角度と辺の長さ」の関係を表した関係式「余弦定理」についてご紹介します。

余弦定理とは？

以下のような三角形ABCがあるとします。

頂点Bはxy座標上の原点Oとして、辺BCはx軸の正の部分と一致するとします。

このとき正弦定理と同じく、頂点Aの内角$\angle BAC$をA、頂点Bの内角$\angle CBA$をB、頂点Cの内角$\angle ACB$をCとして、その対辺をそれぞれa、b、cとします。

また頂点Aから辺BCに垂線を下ろし、BCとの交点をHとします。

直角三角形ABHに着目すると、辺AHと辺BHは三角比を使うと以下の式で表すことができます。
$ \sin B=\dfrac{AH}{AB}=\dfrac{AH}{C} $
$ AH=c\sin B $

$ \cos B=\dfrac{BH}{AB}=\dfrac{BH}{C} $
$BH=c\cos B$

$BC=BH+CH$かつ$BC=a$なので
$CH=a-c\cos B$

次に直角三角形ACHに着目して、AC、AH、CHに三平方の定理を使うと、以下になります。
$AH^2+CH^2=AC^2$

$(c\sin B)^2+(a-c\cos B)^2=b^2$

$c^2\sin^2 B+a^2-2ac\cos B+c^2\cos ^2B=b^2$

$c^2(\sin^2B+\cos^2B)+a^2-2ac\cos B=b^2$

$b^2=c^2+a^2-2ac\cos B$

他の辺も同様に表すことができるので、以下のように三角形の辺とcos(＝余弦) を使った関係式で表すことができます。

$a^2=b^2+c^2-2bc\cos A$
$b^2=c^2+a^2-2ca\cos B$
$c^2=a^2+b^2-2ab\cos C$

これを余弦定理と言います。

またこの式は、以下のように変形して使うこともあります。

$\cos A=\dfrac{b^2+c^2-a^2}{2bc}$

$\cos B=\dfrac{c^2+a^2-b^2}{2ca}$

$\cos C=\dfrac{a^2+b^2-c^2}{2ab}$

この式により三角形の三辺がわかれば、角度を求めることができます。

以上、余弦定理の公式と、その変形させた式をご紹介しました。

それでは実際に余弦定理を使って、三角形の辺の長さや角度を求める問題を見てみましょう。

余弦定理の例題

＜例題１＞
⊿ABCにおいて、$a=3,b=5,C=120^{ \circ } $のとき、cの長さを求めよ。

---

⊿ABCは以下のような三角形になります。

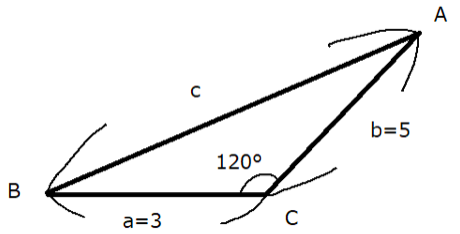
三角形の2辺a、bとその間の内角Cがわかっているので、余弦定理を使います。
$c^2=a^2+b^2-2ab\cos C$
$c^2=3^2+5^2-2\times3\times5\times\cos 120^{ \circ }$
$c^2=9+25-30\times(-\dfrac{1}{2})$
$c^2=49$
$c \gt 0$より$c=7$

＜例題2＞
⊿ABCにおいて、$a=7,b=5,c=8$のとき、Aを求めよ。

---

⊿ABCは以下のような三角形になります。

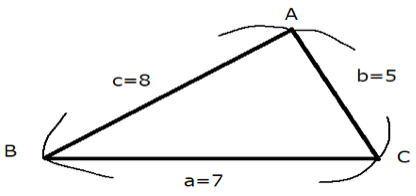
この問題のように三角形の3辺の長さが与えられているときには、内角を求めるために以下の余弦定理を変形した式を使います。

$\cos A=\dfrac{b^2+c^2-a^2}{2bc}$

この式に問題文からわかる値a=7,b=5,c=8 を代入すると
$\cos A=\dfrac{5^2+8^2-7^2}{2 \times 5 \times 8}$

$\cos A=\dfrac{40}{80}$

$\cos A=\dfrac{1}{2}$

したがって$A=60^{ \circ }$

cosを使う余弦定理で角度を求める際には、必ず符号を確認して、問われている角度が第一象限にあるのか、第二象限にあるのかを判別しましょう。

最後に

このように新たな公式「余弦定理」は、三角形のcosの値や関連する辺の長さを求めるのにとても便利な公式です。

正弦定理と同じく、問題を解くときには、図を描いてみて、その時点で何の値がわかっているのか、何の値が求められているのかを確認しましょう。

******************************
全国対応！高校数学・物理化学専門の
オンライン家庭教師・個別指導学習塾、
栃木県宇都宮市近辺の家庭教師を
お探しならこちらをクリック
↓　↓　↓