【数学1】図形と計量(三角比)⑧三角比を用いた三角形の面積の求め方


【数学1】図形と計量(三角比)⑦余弦定理とは?その証明と2パターンの使い分け からの続き
前回までは三角比を使って、三角形の辺の長さや角度を出すための公式をお伝えしてきました。
今回はこれまでお伝えしてきた三角比を使って、三角形の面積を出す公式と内接円の半径を出す公式についてご紹介します。
正弦定理と余弦定理と合わせて、三角比の知識を応用して様々な図形に関する問題を解くために必要な公式なので、しっかり頭に入れましょう。
三角比による三角形の面積の公式
まずは三角形の面積を出す公式の求め方をご紹介します。
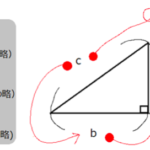
下図のような⊿ABCがあり、その頂点A,B,Cの対辺をそれぞれa,b,cとします。
また頂点Aから辺BCに下した垂線と交わる点をHとします。
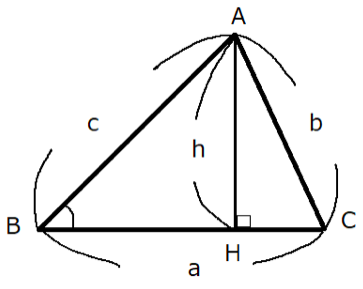
$\angle B$が鋭角もしくは直角$(0^{ \circ } \lt B \leqq 90^{ \circ })$であるとき、$\sin B$は以下のように表すことができます。
$\sin B=\dfrac{h}{c}$
$h=c\sin B$
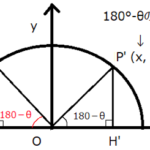
また下図のように$\angle B$が鈍角$(90^{ \circ } \lt B \leqq 180^{ \circ })$であるとき
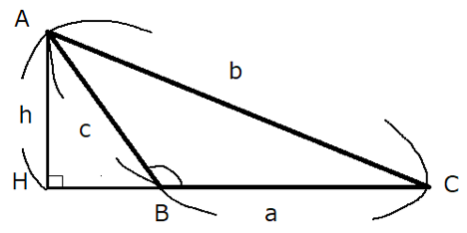
$\sin B$は以下のように表すことができます。
CBを延長した直線とAから下した垂線が交わる点をHとします。
このとき$\angle ABH=180^{ \circ }-B$なので、鋭角と同様にhをsinで表すことができます。
$\sin (180^{ \circ }-B)=\dfrac{h}{c}$
$\sin B=\dfrac{h}{c}$
$h=c\sin B$
よって$\angle B$は鋭角、直角、鈍角いずれの場合でも$h=c\sin B$と表すことができることが分かります。
$S=\dfrac{1}{2}ah$
$S=\dfrac{1}{2}ac\sin B$
$\angle A$、$\angle C$も同様に計算できるので、三角形の面積は以下の公式により求めることが出来ます。
$S=\dfrac{1}{2}ab\sin C=\dfrac{1}{2}bc\sin A=\dfrac{1}{2}ca\sin B$
三角形の面積と内接円の半径
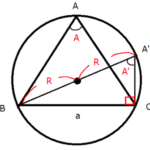
下図のような三角形があるとします。
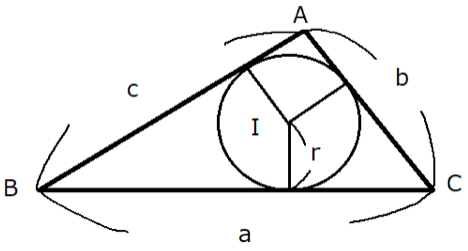
この時⊿ABCの各辺a,b,cと接する円が三角形の内部にあります。
ちなみにこのような円を内接円といい、各辺から等距離にある内接円の中心を内心といいます。
ここでは内心を$I$とします。
このとき内心$I$から各辺に下ろした垂線との交点までの長さは、内心円の半径と等しくなります。
この半径をここでは$r$とします。
さらに各頂点A,B,Cから内心に直線を伸ばします。
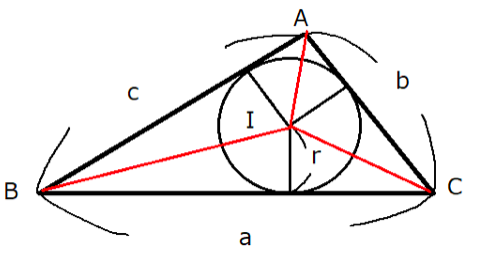
すると$⊿ABC$は$⊿IAB,⊿IBC,⊿ICA$の3つの三角形から構成されていることが分かります。
そしてこれら3つの三角形の面積は以下の式で求めることができます。
$⊿IAB=\dfrac{1}{2}cr$
$⊿IBC=\dfrac{1}{2}ar$
$⊿ICA=\dfrac{1}{2}br$
⊿ABCの面積Sはこれら3つの三角形から構成されているので、その面積は以下の式で求めることができます。
$S=\dfrac{1}{2}cr+\dfrac{1}{2}ar+\dfrac{1}{2}br$
$S=\dfrac{1}{2}(a+b+c)r$
以上三角比を使って三角形の面積を求める公式と、三角形の内接円の半径を求める公式をご紹介しました。
では実際に例題を解いてみましょう。
三角形の面積と内接円の半径を求める例題
<例題>
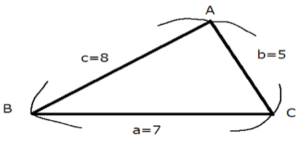
$⊿ABC$において$b=6,c=5,\cos A=\dfrac{1}{5}$のとき、辺$a$の長さと$⊿ABC$の面積$S$、$⊿ABC$の内接円の半径$r$を求めよ。
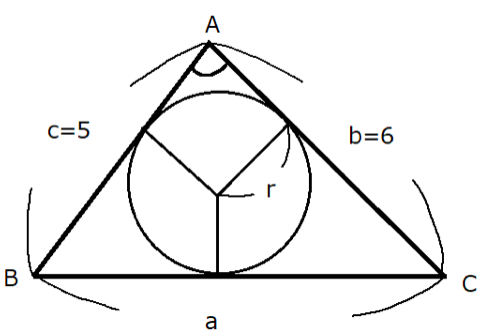
<解答>
2辺とその間の角度Aの三角比が与えられているので、まずは辺aを求めるために余弦定理を使います。
$a^2=b^2+c^2-2bc\cos A$
$a^2=6^2+5^2-2 \times 6 \times 5\times \dfrac{1}{5}$
$a^2=49$
$a \gt 0$より$a=7$
⊿ABCの面積は以下の三角形の面積を求める公式より求められます。
$S=\dfrac{1}{2}bc\sin A$
ここで
$\sin^2 A+\cos^2 A=1$より
$\sin^2 A=1-\cos^2 A$
$\sin^2 A=1-\left( \dfrac{1}{5} \right)^2$
三角形の内角の和は180°なので、$\angle A$も$180^{ \circ }$以下です。
よって$\sin A$は必ず正になるので
$\sin A=\dfrac{2\sqrt{6}}{5} $
したがって
$S=\dfrac{1}{2} \times6 \times5 \times\dfrac{2\sqrt{6}}{5} $
$S=6\sqrt{6}$
次にここで分かった三角形の面積を、内接円の半径を求める公式に代入します。
$S=\dfrac{1}{2}(a+b+c)r$より
$6\sqrt{6}=\dfrac{1}{2}(5+6+7)r$
$18r=12\sqrt{6}$
$r=\dfrac{2\sqrt{6}}{3}$
このように三角形の面積の問題では、2辺の長さと2辺に挟まれた角度のsinが分かれば求めることができます。
問題文でsinの値や具体的な角度が与えられていない時には、余弦定理からcosを導いてsinの値を出すことができます。
問題文からどの辺、どの角度、どの三角比について値が与えられているか、そしてその値を使える公式は何かを順序だてて考えていくと、必要な公式に辿り着くことができるでしょう。
今日学んだ三角形の面積の公式と内接円を導く公式は、正弦定理と余弦定理と組み合わせた応用問題がよく出されます。
基礎を押さえておけば、四角形や外接円が登場する応用問題も解けるので、しっかりと抑えておきましょう。
******************************
全国対応!高校数学・物理化学専門の
オンライン家庭教師・個別指導学習塾、
栃木県宇都宮市近辺の家庭教師を
お探しならこちらをクリック
↓ ↓ ↓