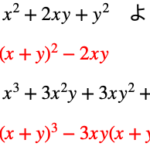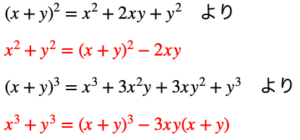【数学Ⅰ】たすき掛けによる因数分解〜組み合わせを楽にみつける方法


高校でまず新たに学ぶことと言えば
たすき掛けによる因数分解があります。
その組み合わせを見つけるのも
最初は苦労するでしょう。
「慣れればすぐ見つかるようになる」
と、学校の先生は言うかもしれません。
ですが慣れとは関係なしに
たすき掛けの組み合わせを
見つけやすくするコツはあります。
今回はたすき掛けのやり方から
たすき掛けのコツまで
ご紹介していきます。
①たすき掛けのやり方
例題1
次の式を因数分解しなさい。
![]()
①まずx2の係数の3の積の形を考えます。
これは正の整数に限定すれば
1✕3しかありませんね。
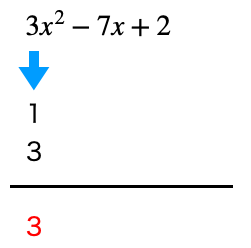
②次に定数項の2の積を考えます。
候補としては
1✕2、(−1)✕(−2)
2✕1、(−2)✕(−1)
などがあります。
それらを図のようにたすきのように配置して
掛け算していきます。
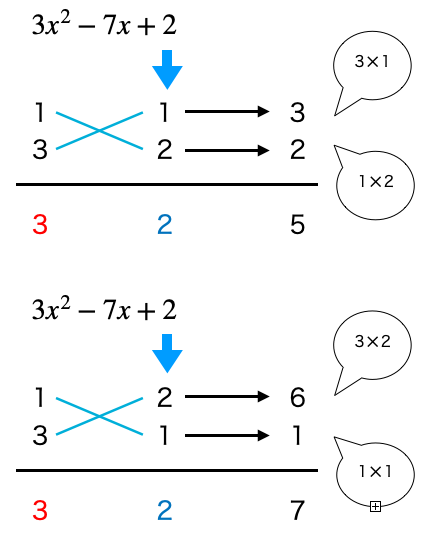
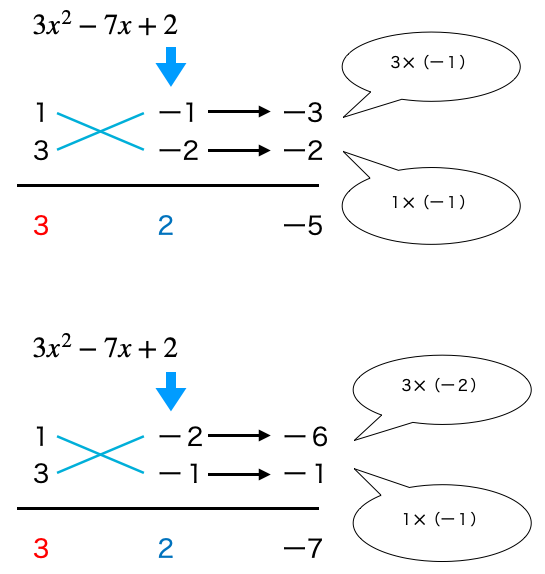
右の積の和を下に書きますが、
この和がxの係数と一致しているものが
該当するたすき掛けの組み合わせです。
この例題の場合は
一番最後の組み合わせが一致してますね。
この場合(x-2)と(3x-1)が因数になります。
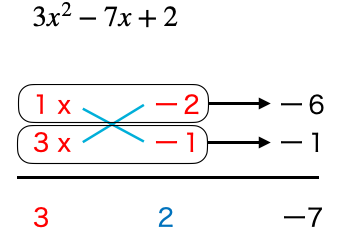
したがってこの例題は
このように因数分解できます。
![]()
②たすき掛けの組み合わせを簡単に見つける方法
たすき掛けの組み合わせは慣れれば
すぐに見つかると言われます。
しかし、これからお伝えする
コツを意識すれば、慣れとは関係なしに
簡単に見つけることができます。
例題2
次の式を因数分解せよ
![]()
この場合、次の4通り考えられます。
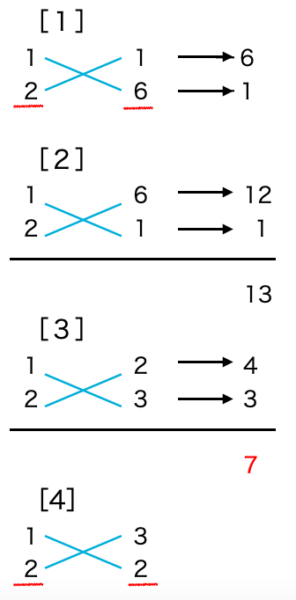
このうち[1][4]には赤線部に
共通因数2がありますが、
元の式の2x2+7x+6は
2でくくれないので
[1][4]は考える必要がありません。
[2][3]でxの係数の7に合うのは
[3]です。
したがって
![]()
となります。
例題1,2の場合
x2の係数と定数項が小さいので
考えられる組み合わせは
それほど多くありません。
しかし、それらが大きくなると
掛け算の組み合わせが増えて
たすき掛けの組み合わせも増えていきます。
そういう場合にこのコツが効いていきます。
例3
![]()
この場合、
12=22✕3
24=23✕3
なので何も考えずに
たすき掛けの組み合わせを考えると
組み合わせの数が多くなります。
しかし、先程のコツを利用すれば
楽になります。
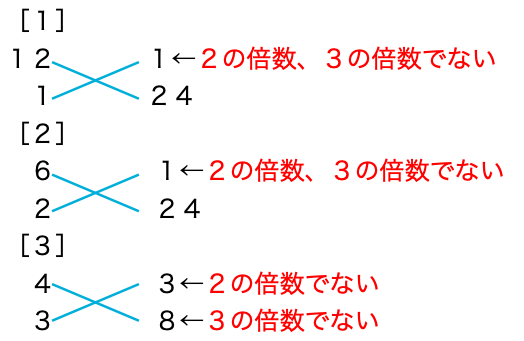
これらの3通りが考えられますが
[1][2]の場合、
xの係数が大きくなりすぎます。
また[3]の場合も
共通因数が出てこないようにすると
すぐに答えがわかります。
したがって
![]()
となります。
たすき掛けによる因数分解は
高校では頻繁に使うことになります。
というか、たすき掛けができないと
高校数学でやっていけません。
今回お伝えしたコツも意識して
早めにマスターしましょう。
******************************
高校数学・物理化学専門の
オンライン家庭教師・個別指導学習塾、
栃木県宇都宮市近辺の家庭教師を
お探しならこちらをクリック
↓ ↓ ↓