二次方程式解き方と解の公式、判別式と二次関数の共有点の個数の関係


中学生の時に学習したように、
二次方程式とは、
ax2+bx+c=0 の形をした式のことでした。
(a,b,cはそれぞれ実数でa≠0)
二次方程式は基本的に
次のいずれかの方法をとることによって
解くことが出来ます。
①平方完成 ➁因数分解 ③解の公式を利用
なぜこれらを使うことで求められるのか
どのように使うのかなどを
それぞれの場合で見ていきましょう。
また記事後半では
二次方程式の判別式と
二次関数の共有点の個数について
学んでいきましょう。
1.二次方程式の解き方
①平方完成で二次方程式を解く
これは次の事実を使うことで
二次方程式を解こうというものです。
![]()
因数分解や解の公式のほうが
使う機会が多いからなのか、
これを忘れている高校生は非常に多いです。
しかし、これを知らないと、
とても計算が大変になることが
よくあるので、ぜひ覚えておいてほしいです。
➁因数分解で二次方程式を解く
これは中学生で習うこともあり、
一番メジャーな解き方だと思います。
そのためここでは
具体的な解き方というより、
なぜ因数分解をすれば
二次方程式が解けるのか?
ということをお話ししたいと思います。
それは、因数分解をすることによって
![]()
が使えるようになるからです。
掛けて0と言うことは、
少なくとも1つは0であるということを
用いているわけです。
だから因数分解をして
二次方程式を解くときは
![]()
というように各因数が0になるように
xを定めるわけですね。
③二次方程式の解の公式を使って解く
二次方程式の解の公式は次のようなものでした。

①は中学で学びましたが
②は高校で新たに学ぶ解の公式です。
②は使わなくても計算を頑張れば
①だけで解けます。
しかし、受験レベルなど難易度が高くなると
②が使えるときは使った方がいいです。
ちなみに解の公式は
平方完成して①の方法で解いていくと
導けます。
例題
それでは何問か実際に解いてみましょう。
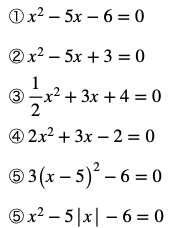
解答


2.判別式
ここからは先ほども登場した
二次方程式の解の公式について
少し詳しく見ていきましょう。
二次方程式の解の公式には
非常に重要な性質が隠れています。
それは
「根号の中身の符号によって
二次方程式の解の個数が分かる」
ということです。
符号と言いましたが、
正確には根号の中身が
正か0か負かに分けられます。
そしてこの根号の中身、
つまりb2ー4ac は
とてもよく使うため、
毎回同じ式を書かなくて済むように
Dという記号でよく表します。
そしてこのb2ー4ac を、
その二次方程式の判別式と言います。
Dの値によって二次方程式の解の個数は
次のように分けられます。
D>0のとき:異なる2つの実数解を持つ。
D=0のとき:1つの実数解(重解)を持つ。
D<0のとき:実数解は持たない。(異なる2つの虚数解を持つ)
このうち、実数解を持つ
D>0とD=0をあわせて
「D≧0↔実数解を持つ」
とすることもよくあります。
というのは根号の中身が負になるので
実数の世界では許さないからです。
それでは先ほどの問題を使って
今度は解の個数だけを
判別してみましょう。

3.判別式による二次関数とx軸との位置関係
・判別式と共有点の個数
二次関数のグラフとx軸との位置関係は
それらの共有点の個数によって
次の3つに分類することが出来ます。
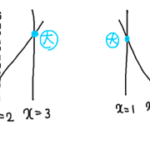
①異なる2つの共有点を持つ
②ただ1つの共有点を持つ
③1つも共有点を持たない
図を書くと次のようになります。
グラフの色と①~③の文字の色が対応しています。
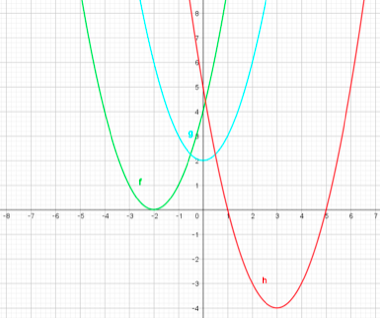
さて、この分類は
幾何的(図形的、見た目で分かる特徴)な
分類になっています。
このような幾何的なイメージも
非常に大事ですが、
それと同じくらい数式で
この特徴を捉えることも大切です。
共有点と言うのは
数式的には連立方程式の実数解です。
よって、
![]()
の共有点のx座標というのは、連立方程式
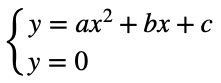
すなわち二次方程式
![]()
の解ということになります。
ということは、
二次関数のグラフとx軸との
共有点の個数を知りたければ、
この二次方程式の実数解の個数を
調べればよいということになります。
二次方程式の実数解の個数は
いちいち解を求めなくても
「判別式」を使えば求まりました。
ということで以上の話をまとめると
次のようになります。

ちなみに共有点と言うのは
交点や接点のことです。
・例題
では2問例題を解いてみましょう。
まずは簡単な問題です。
(例題1)
y=x2+ax+4がx軸と接するようなaの値を求めよ。
解答:
接すると言われたので
二次方程式y=x2+ax+4 が
ただ1つの実数解を持つ、
すなわち判別式D=0なら良い
ということになります。
よって
![]()
これを解くとa=±4 となり
これが答えです。
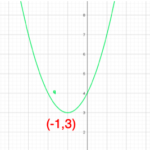
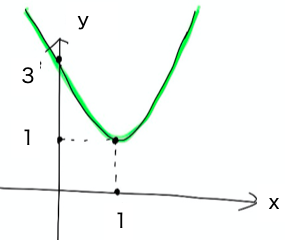
ちなみにa=4の時のグラフは
先ほどの図の緑のグラフです。
次はこれまでの二次関数に関する知識を
いろいろ使って解く問題です。
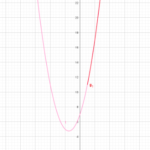
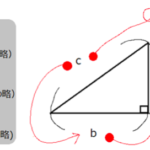
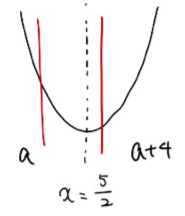
(例題2)
y=x2+bx+cのグラフが
図のようになるとき、(1)~(6)の符号を答えよ。
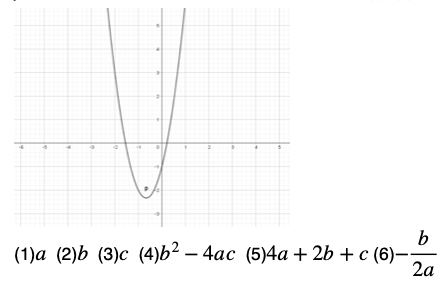
解答:

ちなみにこの問題で出したグラフは
y=3x2+4xー1
のグラフです。
実際にa,b,cに3, 4, -1を代入して
(1)~(6)の符号を確かめて
あっていることが確認できます。
また、解答の途中で出てきた
![]()
については非常によく出てくるので
覚えておくと便利です。
二次関数の平方完成を行えば
簡単に証明することが出来ます。
平方完成について簡単に触れておきます。

まとめ
二次方程式は中学でも学びましたが
高校で初めて学ぶ
xの係数bが偶数の時の
解の公式は計算が楽になるので
ぜひ使うようにしましょう。
さらに後半で説明した判別式や
判別式と共有点の個数の関係は
高校数学で使う機会は非常に多いので
この機会にマスターしてくださいね。
******************************
全国対応!高校数学・物理化学専門の
オンライン家庭教師・個別指導学習塾、
栃木県宇都宮市近辺の家庭教師を
お探しならこちらをクリック
↓ ↓ ↓