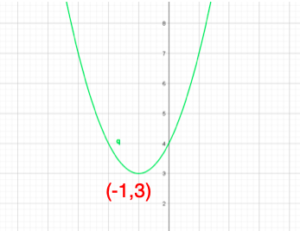
二次関数の最大値最小値の求め方(定義域がない場合と定義域がある場合)


二次関数のグラフと平方完成、グラフの平行移動が置き換えでできる理由からの続き
二次関数では最大値と最小値を求めることをよく行います。(数IIや数IIIへ学習を進めると三次関数や四次関数などの一般の曲線でも行います)
二次関数で最大値や最小値が存在する時、その求め方は非常に簡単なことが多いです。
問題を通して、最大値・最小値の求め方を見ていきましょう。
1、二次関数の最大値・最小値
定義域と値域
具体的な問題を通して解き方を見ていく前に、高校で初めて使う用語の解説です。
中学の二次関数ではx,yの取る範囲をそれぞれxの変域、yの変域と言っていましたが、高校からはxの取る範囲を定義域、yの取る範囲を値域と呼びます。
例題)二次関数の最大値・最小値
次の二次関数が最大値・最小値を持つなら最大値・最小値を求めよ。また、その時のxの値も求めよ。
![]()
解答)
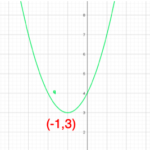
① 平方完成すると
![]()
下に凸なグラフなので

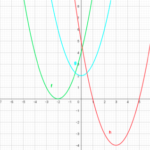
②これは原点を頂点に持つ二次関数
![]()
をy軸方向に5平行移動したグラフである。
よってx=0で最小値5を取る。最大値は持たない。
③平方完成すると
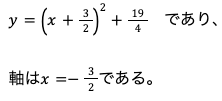
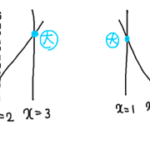
今定義域が1≦x≦5なので関数は図のようになる。
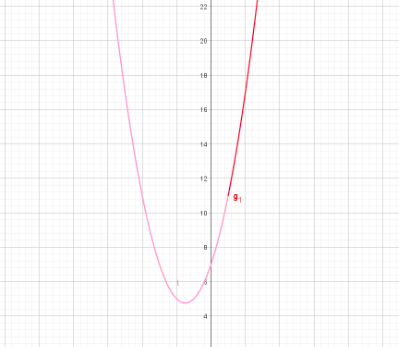
(薄いピンクの線は定義域がなかった時のグラフ)
よって
x=1で最小値11を、
x=5で最大値47を取る。
補足:基本的に二次関数の最大・最小は平方完成をすることで軸と頂点の座標を求めることで存在するかしないかの判断も含めて探していきます。
2、定義域と二次関数の最大値、最小値
定義域のない二次関数
☆y=ax2+bx+cの場合
・下に凸(a>0)ならば二次関数は軸の位置で最小値を取り、その値は頂点のy座標になる。最大値は取らない。
・上に凸(a<0)ならば二次関数は軸の位置で最大値を取り、その値は頂点のy座標に等しい。最小値は取らない。
ということが言えます。図を書いてみれば一目瞭然です。
定義域がある二次関数
同様に定義域がある場合も考えます。これも図を書いていけば分かりますが、
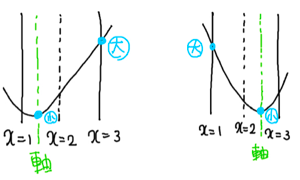
(ⅰ)定義域内に軸がある場合
・下に凸ならば頂点で最大値を取り、軸から遠いほうの定義域の端で最小値を取る。
・上に凸ならば頂点で最小値を取り、軸から遠いほうの定義域の端で最大値を取る。
(ⅱ)定義域外に軸がある場合
・下に凸ならば軸から近いほうの定義域の端で最小値を取り、軸から遠いほうの定義域の端で最大値を取る。
・上に凸ならば軸から近いほうの定義域の端で最大値を取り、軸から遠いほうの定義域の端で最小値を取る。
ということが言えます。
これらは毎回正しく図を描けばすぐにわかるので一言一句覚えておく必要はありません。
しかし、今後さらに難しくなった時(定義域や軸が動く場合)に少し頭にあると良いことがあるので雰囲気位は覚えておいてもいいと思います。
また、問題を解くうえでの注意点ですが、二次関数は必ずしも最大値や最小値を持つとは限りません。
基本的に定義域がなければ最大値か最小値どちらかは絶対に取りませんし、定義域があったとしても定義域の端が含まれていなければ最大値や最小値は取らないこともあります。
例えば例題③で定義域を1<x≦5と変えてみましょう。
x=5で最大値を取るのは変わりませんが、定義域左端をどう扱ったらいいでしょうか。
等号が付いていません。
これは「x=1は含まないけど、どれだけでもx=1に近づけることが出来るよ」という意味です。
つまり「x=1で最小値を持つ」とは言えないのです。
かといって最小値を取る点を特定できるわけではありません。
1に物凄く近い点で
最小値っぽい値を取ることはわかるので、
仮にその「物凄く近い点」を
1.000001と選び、
この点で最小値を取ると
答えたとしましょう。
1にとても近い数なのでよさそうですが、これはダメです。
それは今選んだ1.000001より
はるかに1に近い数、例えば
1.0000000000000000001が取れるからです。
こんな感じで定義域の端が含まれていない時は無理に最小値、最大値を取る場所を決めても絶対にもっと最大、最小を取るにふさわしい点が現れてしまうので最大値や最小値は存在しないのです。
非常に高度な話にはなってしまいましたが、これを理解しておかないと簡単に引っかかってしまう罠なので頑張って理解してみてください。
******************************
全国対応!高校数学・物理化学専門の
オンライン家庭教師・個別指導学習塾、
栃木県宇都宮市近辺の家庭教師を
お探しならこちらをクリック
↓ ↓ ↓