二次関数の最大値・最小値を求めるうえで、毎回必ず全ての係数が分かっているとは限りません。

ここではそのような二次関数の最大値・最小値の求め方について見ていきます。

必要な知識は平方完成くらいですので早速例題を通して見ていきたいと思います。

１、文字を含む二次関数の最大値・最小値

（例題１）

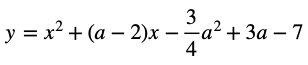
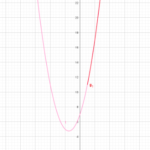
の最小値をmとする。

最小値mをaの式で表し、mの最大値を求めよ。

---

解答：まずは二次関数の最小値mを求めるので平方完成です。

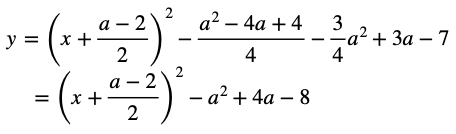
これは下に凸な関数なので

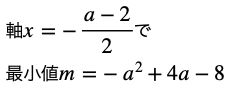
を取ります。

これが前半部分の解答です。

続いて後半部分は今求めたmが新たに二次関数として出てきたので、これの最大値を求めなさいということです。

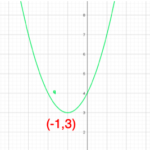
同じようにmを平方完成していきます。

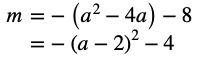
mは上に凸な関数なので軸ａ＝２で最大値−４を取ります。

これが後半の答えです。(問題で聞かれなくてもａが何のとき、最大値or最小値を取るのかも明記しましょう)

２、文字を含む二次関数の最大値・最小値（定義域がある場合）

それでは少し難易度を上げます。

次は高校数学全体の中でもトップクラスに重要なことです。

2次関数の定義域や軸など種々の要素を自由に動かせる状況で最大値・最小値を求めるということをしていきます。

このレベルになると毎回何が動いて何が固定されているのか明確に図示していかなければなりません。

公式の暗記などでは到底解くことが出来ない類の物です。

百聞は一見に如かずと言うことで例題を見てみましょう。

（例題２）

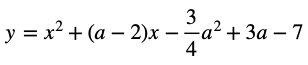
（１≦ｘ≦３）の最大値と最小値を求めよ。

---

解答：先ほどと同じ式なので省略しますが平方完成すると

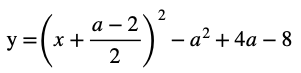
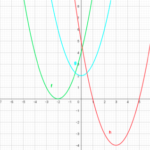
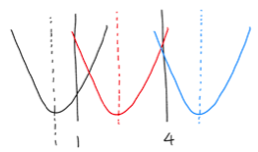
さて、aというイレギュラーな文字があるので今動くものは何で動かないものは何かと言うことを見分けます。

今、定義域は動くでしょうか。

答えは「動かない」ですね。

定義域は１≦ｘ≦３と固定されています。

では軸はどうでしょうか。

もちろん「動く」が答えです。

文字aが入っていますから、aの値によって軸はあっちへ行ったりこっちへ行ったりするわけです。

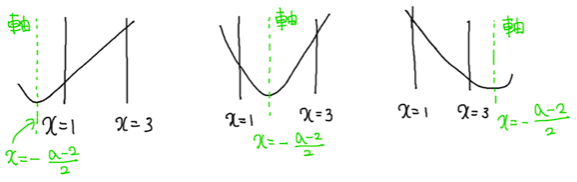
なので最大値・最小値を求める際、軸の位置で場合分けしなければならなそうですね。

（軸が定義域の外側や定義域内どこにあるかで最大・最小値は変わるからです。）

他に動くものはあるでしょうか。

まあ頂点のy座標は動きそうですが、それは軸上にある点なので軸の位置で場合分けすればあまり気にしなくてよさそうです。

ということで軸の位置だけで場合分けすればよさそうで、なおかつ軸が

①定義域の外側　➁定義域の内側 に分ければよさそうだと分かりました。

①はさらに二つに分解できますね。（今回なら1より小さいほうの外側と3より大きいほうの外側）

後はこれを実践していくだけです。

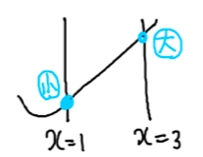
さて、ここで新たに問題が発覚したように思われますね。

最大値を求めたいのですが、最大値が一つに定まらなそうです。

軸から遠いほうの定義域の端で最大値を取りますが、どっちのほうが遠いかなんてこれまでの情報じゃわからないですからね。

なのでここで追加の場合分けをします。

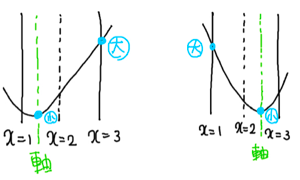
（ⅱ）ー１ 軸が定義域の中央ｘ＝２よりも小さく,ｘ＝１より大きいとき

（ⅱ）ー２ 軸が定義域の中央ｘ＝２よりも大きく、ｘ＝３より小さいとき

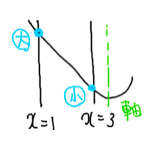
以上で全て求めることが出来ました。
最後に結果だけまとめて終わりです。

******************************
全国対応！高校数学・物理化学専門の
オンライン家庭教師・個別指導学習塾、
栃木県宇都宮市近辺の家庭教師を
お探しならこちらをクリック
↓　↓　↓