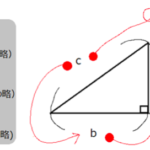
二次関数の最大値・最小値／区間（定義域）が固定されて軸が動く場合

文字を含む二次関数の最大値・最小値の求め方（グラフによる場合分け）からの続き

 

二次関数の最大値・最小値を求める問題で最も重要なのは「定義域や関数が動くときの最大値・最小値」を求める問題です。

この問題は丸暗記では太刀打ちできず、理屈を理解した上で正しく論理的に考え答えを導き出せるかという力が問われます。

逆に言えばこの問題が解けるようになればそのような力が付いてきているということになるので、高校数学全体でも重要といって過言ではありません。

必要な知識は「平方完成」、「平方完成した式を見てグラフを書く」の二つです。

さっそく例題から見ていきましょう。

１、軸が動く二次関数の最大値・最小値

例題：

（１≦ｘ≦４）の最小値と最大値を求めよ。

---

解答：二次関数の最大値・最小値と来たら何はともあれ平方完成です。

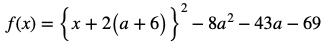
今回は関数の軸がaの値によって変わりそうです。

しかし区間（定義域）は固定されていますね。

なので今のところ軸は位置が決まるということはありません。

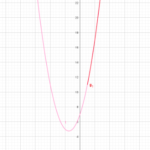
それを踏まえるとこの式から図のようなグラフが書けます。

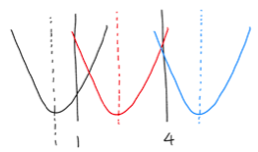
このように区間の外側に軸がある場合と内側にある場合で大きく3パターンに分かれそうです。

ここまで準備したうえで最小値から求めてみましょう。（最大値と最小値は一気にではなく分けて考えた方がやりやすいです。）

最小値

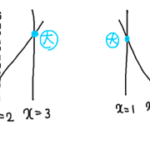
(1)　軸が区間の左にある場合、つまり

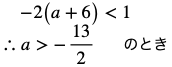
下図よりｘ＝１で最小値

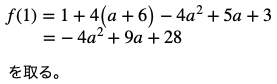
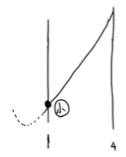
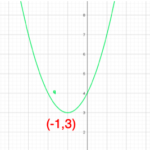
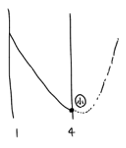
(2) 軸が区間の中にある場合、つまり

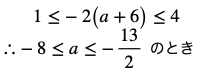
下図よりｘ＝ー２（ａ＋６）で最小値

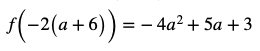
を取る。

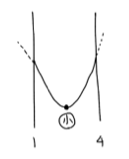
(3) 軸が区間の右にある場合、つまり

下図よりｘ＝４で最小値

を取る。

最大値

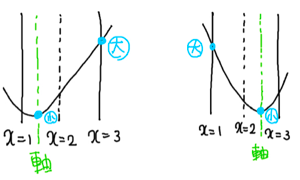
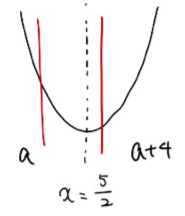
(1) 軸が区間の中央にある場合、つまり

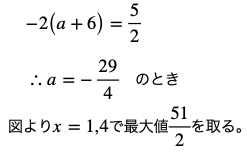
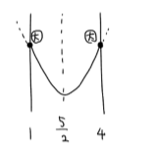
(2) 軸が区間の中央

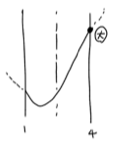
(3) 軸が区間の中央

 

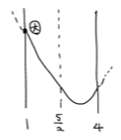
２、軸が動く二次関数の最大値最小値の求め方のまとめ

以上が軸が動く二次関数の最大値最小値の求め方です。

慣れないうちは非常に難しく感じると思いますが、やること・考えることはいつも同じです。

①平方完成する
②軸、定義域など何が動いて何が動かないのか確認する
③動かないものをとりあえず図示
④動くものを動かしてどこで場合分けするか考える
⑤場合分けしたらそれぞれの場合ごとに図を書いて最大値・最小値を取る場所を求める。

基本的な流れはこうなります。

先ほどの例題の解答と照らし合わせると実感しやすいです。

一番難しいのは④だと思うので、④の考え方をもう少し詳しく見ていきましょう。

先ほどの例題を使います。

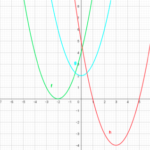
まずは最小値ですが、これは軸が区間（定義域）の外か中かで３つに場合分けしました。

これはどのように見つけたかというと、固定されている区間（定義域）の図だけ書いて、そのうえでグラフ（動くもの）を頭の中でちょっとずつ動かしていっただけです。

そうすると軸がの両端をまたぐ瞬間だけ最小値を取る場所が変わることに気付きます。

---

＊念のため補足ですが、例えば軸が区間の左より小さい所にあるとして、そこからさらに軸を左に動かしても最小値はｘ＝１で取ることに変わりはありません。

軸が区間内にある時も軸が区間内で動けば最小値自体は変わりますが、頂点が最小値になるというのは変わりません。

---

 

最大値も同じように、地道に頭の中でグラフを動かしてどこで最大値の取り方が変化するかを探して、この場合分けでいいことに気付きました。

はじめのうちは頭でイメージするのは難しいかもしれないので、ちょっとずつグラフをずらしたものを実際に書いて調べるのもいいです。

慣れてくると場合分けのコツが分かってそんなに考えなくても見当がつくようになります。

 

******************************
全国対応！高校数学・物理化学専門の
オンライン家庭教師・個別指導学習塾、
栃木県宇都宮市近辺の家庭教師を
お探しならこちらをクリック
↓　↓　↓