【数学A】場合の数と確率⑨事象と確率、余事象、積事象と和事象の確率


【数学A】場合の数と確率⑧同じものを含む順列と重複組合せによる並べ方 からの続き
ここでは確率の基礎と「余事象」「和事象」などについて説明していきます。
確率とは実験や観測の結果で、実験や観測のことを試行といいます。
また試行の結果起こる事柄を事象といいます。
例えばある事が起こる確率が
![]()
2回に1回起こると考えるよりも
2万回の試行をしたら
あることが1万回くらい起こることだとみなします。
確率の定義
では例題を見ながら確率の基本用語を見ていきましょう。
【例題1】1個のサイコロを投げる試行で、偶数の目が出る確率を求めよ。
(解答)1つの試行で起こり得る結果全体を集合Uで表すとき、U自身で表される事象を全事象という。
ここでは
U={1,2,3,4,5,6}
偶数が出るという事象をAとすると
A={2,4,6}
また、Uのただ1つの要素からなる集合で表される事象を根元事象という。
ここでは根元事象は
{1},{2},{3},{4},{5},{6}
試行において、どの根元事象が起こる事が同程度に期待できるとき、同様に確からしいといい、この問題の場合もサイコロの目の出方は同様に確からしいと言える。
このとき事象Aが起こる確率を
P(A)と表し、次の式が成り立つ。

この問題を上の式に当てはめると
n(U)=6、n(A)=3なので

余事象の確率
全事象をUとした時、事象Aに対して「Aが起こらない」事象をAの余事象といい、Āで表す。
余事象Āの確率について、次式が成り立つ。
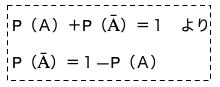
【例題2】
10本の内3本の当たりが入っているクジがある。
この中から同時に2本引くとき、少なくとも1本が当たりの確率を求めよ。
(解答)
この問題では、「少なくとも1本あたり」は「2本ともハズレ」の余事象になる。
10本の中から2本引く場合の数は
10C2=45 通り
「2本ともハズレ」の場合の数は
7C2=21 通り
よって求める確率は

和事象の確率
一般的に事象A、Bにおいて
・積事象
AとBがともに起こる事象で
A∩Bで表す。
・和事象
AまたはBが起こる事象で
A∪Bで表します。
・排反事象
AとBが同時に起こらない時、事象AとBは互いに排反であるという。
【例題3】
20本のクジの中に当たりが5本ある。
このクジをA、B、2人がこの順に1本ずつ引くとき、A、Bそれぞれが当たる確率を求めよ。
(解答)
Aが当たる確率は
![]()
次にA,Bの順にクジを引く場合の数は20P2=380通り
このうちBが当たる場合の数は
①Aが当たりBも当たる場合
5×4=20通り
②Aが外れBが当たる場合
15×5=75通り
①と②は同時に起こらない、すなわち互いに排反なので、確率の加法定理より、Bが当たる確率は
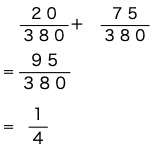
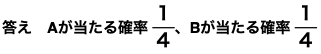
【例題4】
カードが7枚あって、4枚は赤色で、1,2,3,4の数字が書いてある。残りの3枚は白色で、0,1,2の数字が書いてある。これらを横に並べる時、次の確率を求めよ。
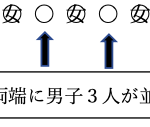
(1)赤、白2色が交互に並ぶ確率
(2)同じ数字はすべて隣り合う確率
(3)同じ数字が隣り合わない確率
(解答)
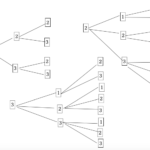
7枚を1列に並べる場合の数は7!通り
(1)赤、白2色が交互に並ぶ場合の数は4!×3!通りなので、求める確率は
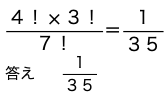
(2)赤の1と白の1、赤の2と白の2をそれぞれ1組と考え、その組の中で動かすので、並べ方は
5!×2!×2!通り
よって求める確率は
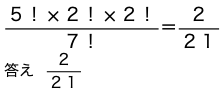
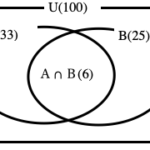
(3)全事象をU、赤の1と白の1が隣り合う事象をA、赤の2と白の2が隣り合う事象をBとすると
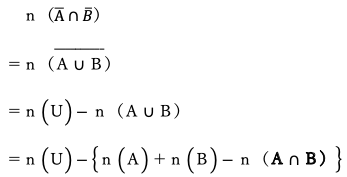
また
n(A)=n(B)=6!×2!
さらに(2)より
n(A∩B)=5!×2!×2!
よって
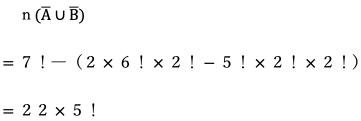
したがって求める確率は
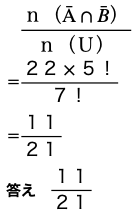
今回は集合の基礎「余事象」「和と積事象」について解説しました。
用語がたくさんありますので、今後のためにしっかりと覚えておきましょう。
******************************
全国対応!高校数学・物理化学専門の
オンライン家庭教師・個別指導学習塾、
栃木県宇都宮市近辺の家庭教師を
お探しならこちらをクリック
↓ ↓ ↓