【数学A】場合の数と確率⑪反復試行の確率の基本と応用

今回は反復試行の確率について説明していきます。

反復試行の確率とは？

その前に確率についての基本的な用語を2つおさらいしておきます。
・確率：結果がどうなるかは断言できない何かしらの実験（試行）をした場合、ある結果が起こる割合
・事象：試行の結果起こりうる結果すべて

少し具体例で考えてみます。

例えばさいころを1回投げるときそれは試行ということができます。

「次投げたら絶対3が出る」みたいに結果が断言できないからです。

普通のさいころは１から６の目がありますから、事象は「１が出る」「2が出る」…略…「６が出る」の６つとなります。

さいころは基本的にすべての目が同じくらいの確率で出るはずです。

ではそれはどのように調べるのでしょうか。

実はここに確率の考え方が使われています。

「何度も何度もさいころを振って、それぞれの目が出る確率を求める」ということをすると、さいころが均等に作られているか、そうでないかわかってくるのです。

この「何度も何度もさいころを振る」というのが反復試行の例です。

この反復試行での確率の計算について見ていきましょう。

反復試行の確率の求め方

反復試行の確率の厳密な定義は「同じ条件下で全く同じ試行を繰り返す」ということです。

明らかに各回の試行は独立ですから、各回で確率を求めたらそれを単に掛けていけばいいということがわかります。

先ほどのさいころの例は事象が6個あって考えるのが面倒なので少し事象を減らして考えましょう。

さいころを5回投げて各回で偶数が出るか、奇数が出るかを調べるという試行を行います。

この場合、各回の事象は「偶数が出る」「奇数が出る」の２つです。

偶数が出ることをE、奇数が出ることをOと書くことにします。

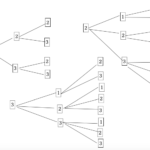
この場合5回投げた結果は
①EEEEE　（5回とも偶数）
②EEEEO
（最初4回連続で偶数、ラスト一回で奇数）
③EEEOE
（最初3回偶数、次に奇数で最後は偶数）
などたくさんのパターンが考えられます。

1回投げて偶数が出る確率は$\frac{1}{2}$、奇数が出る確率は$\frac{1}{2}$

したがって
①の確率は$(\frac{1}{2})^5$
②の確率は$(\frac{1}{2})^4(\frac{1}{2})$
③の確率は$(\frac{1}{2})^4(\frac{1}{2})$
ということになります。

特に②と③を見比べるとわかりやすいですが、②と③はEが4回、Oが1回なので確率の積は常に$(\frac{1}{2})^4(\frac{1}{2})$となります。

あとはEを４つ、Oを１つ並べる並べ方がいくつあるかを考えれば$(\frac{1}{2})^4(\frac{1}{2})$にその並べ方の総数を掛ければEが4回、Ｏが1回出る確率が求まることになります。

これは同じものを含む順列なので$\frac{5!}{4!1!}$となります。

これは組み合わせの定義から${}_5 \mathrm{ C }_4$と書くこともできます。

よって順番は気にせずとにかくＥが4回、Ｏが1回出る確率は${}_5 \mathrm{ C }_4(\frac{1}{2})^4(\frac{1}{2})$ということになります。

これと同じように考えていくと、例えばEが5連続で出る①の場合なら確率は${}_5 \mathrm{ C }_5(\frac{1}{2})^5(\frac{1}{2})^0$となります。

${}_5 \mathrm{ C }_5=1$と$(\frac{1}{2})^0=1$より

${}_5 \mathrm{ C }_5(\frac{1}{2})^5(\frac{1}{2})^0=(\frac{1}{2})^5$となります。

ほかにもEが2回、Ｏが3回出る確率は${}_5 \mathrm{ C }_2(\frac{1}{2})^2(\frac{1}{2})^3$のようになります。

反復試行の確率の公式

これらをじっと見るとある共通点に気づくと思います。

まず${}_5 \mathrm{ C }_2$のような組合せの部分はどれも５回の試行からEが出るタイミングをＥが出た回数分選ぶ総数になっています。

そして${}_5 \mathrm{ C }_2$の2のように組合せCの右側の数字がＥが出る確率$\frac{1}{2}$の指数になっています。

そしてＥでない事象の確率、つまりＯである確率の指数には組合せCの左の数から右の数を引いたものになっています。

ここまでのことを公式のように書くと次のようになります。

---

n回の反復試行である事象Ａが起こる確率をＰ、Ａ以外が起こる確率を（１－Ｐ）とする。この時Ａがk回起こる確率は
$${}_n \mathrm{ C }_k(P)^k(1-P)^{(n-k)}$$

で表される。

---

これからもわかるように、反復試行の確率は○○が起こるか、それ以外が起こるというようにして考えます。

例えばさいころを投げて何の目が出たか調べるという反復試行なら、「10回投げた時に５の目が6回出る確率を知りたい」のように決めて、5の目が出るか、それ以外の目が出るかに分けることになります。

使うさいころがどの目も均等にでるさいころであればこの確率は
$$_{10}\mathrm{ C }_6(\frac{1}{6})^6(\frac{5}{6})^5$$
になります。

反復試行には様々なパターンがありますが、必要な知識は基本的に
$${}_n \mathrm{ C }_k(P)^k(1-P)^{(n-k)}$$
だけです。

あとは問題ごとに考え方を知っていけばおのずと初見の問題でも解けることが多いでしょう。
******************************
全国対応！高校数学・物理化学専門の
オンライン家庭教師・個別指導学習塾、
栃木県宇都宮市近辺の家庭教師を
お探しならこちらをクリック
↓　↓　↓