【数学A】場合の数と確率⑫条件付き確率の基本


【数学A】場合の数と確率⑪反復試行の確率の基本と応用 からの続き
ここでは条件付き確率についてまとめます。
条件付き確率というのは見る世界を狭くした確率です。
もう少し詳しく言えば、普通の確率は「全事象のうち事象Bが起こる割合」を意味するのに対して、条件付き確率は「全事象の中の事象Aが起こった時に、同時に事象Bも起こる割合」ということになります。
条件付き確率とは?
例えば1から6の目があるサイコロを例に考えてみると、1回投げるときの全事象は「1の目が出る」「2の目が出る」…「6の目が出る」の6通りです。
事象Bを「3の倍数が出る」としてみると、事象Bは「3の目が出る」「6の目が出る」の2つです。
事象Bが起こる確率は$\dfrac{2}{6}=\dfrac{1}{3}$ですね。
では事象Aを「2の倍数が出る」としてみましょう。
事象Aは「2が出る」「4が出る」「6が出る」の3通りです。
この時、事象Aが起こった時の事象Bが起こる条件付き確率は事象Aが起こった上で事象Bが起こる確率ということです。
ですので2,4,6のいずれかが出て、かつ3,6のいずれかが出る確率を求めればいいことになります。
すると条件を満たすのは6しかないので、事象Aが起こった上での条件付き確率は$\dfrac{1}{3}$になります。
条件付き確率の具体例
条件付き確率は理解しづらい内容なので、もう少し具体例を見てみましょう。
次のような問題を考えます。
問:40人のクラスで好きな教科に関するアンケート調査を行った。その結果を集計すると、次の事実が判明した。
なおこのアンケートで数学も英語もどちらも好きと答えた人はいなかった。

(1)このクラスからランダムに1人選んだ時、その人が出席番号が偶数でかつ数学が好きな人であった確率を求めよ
(2)このクラスからランダムに選んだところ、その人の出席番号は奇数だった。この人が英語が好きである確率を求めよ。
(解答)
この問題は普通の確率と条件付き確率の違いを表しています。
(1)は人を選んだ際の情報が特にないので条件付きではなく、普通の確率の問題です。
(2)は人を選んだ際の条件が分かるので条件付き確率です。
(1)は条件を満たす人数(場合の数)を起こりうるすべての場合の数で割ればいいので$\dfrac{14}{40}=\dfrac{7}{20}$が答えです。
(2)は条件付き確率で、選んだ人の出席番号が奇数だと分かっているので、(1)より見る世界が狭まります。
(1)ではクラス全員で見ていましたが、その半分の出席番号が奇数の人だけを見ればいいことになります。
(見る世界というのが分かりにくいかもしれませんが、出席番号が奇数の人だけで新しくクラスを作って、その中で英語が好きな人の確率を求めればいいということです。)
ということで求める確率は$\dfrac{14}{20}=\dfrac{7}{10}=0.7$になります。
(補足)
(2)は奇数の人に絞って英語が好きな人の割合を求めましたが、元のクラス全体だと英語好きでありなおかつ奇数の人の割合は$\dfrac{14}{40}=\dfrac{7}{20}$になります。((1)と同じ)
この結果と先ほどの(2)の結果を見比べてみましょう。
$\dfrac{7}{20}=0.35$ $\dfrac{7}{10}=0.7$からわかるように、求めている対象は「奇数であって英語が好き」な人で同じなのですが、先に条件がついているか何もついていないかで確率には大きな差が出ます。
もちろん条件付き確率の方が確率は高くなります。
(奇数であって英語が好きの人数は変わらないまま、条件によって全体の人数が減ったので奇数であって英語が好きな人の割合は高くなる)
図で書くと次のようなイメージです。
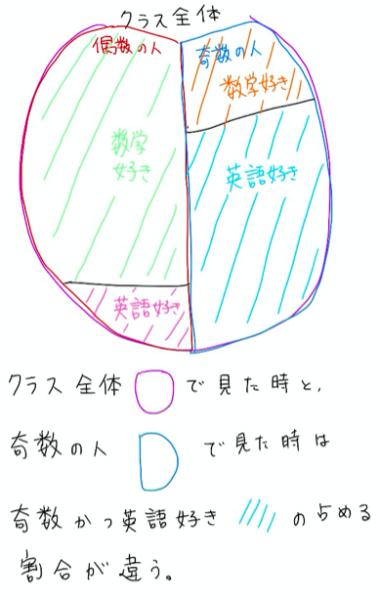
条件付き確率の公式
ここまでは表や具体的に出る目を考えたりして条件付き確率を求めてきましたが、いつでもこれができるわけではありません。
複雑な試行の時は特にこれまでの方法では解きにくくなります。
そのための公式は以下のようになります。
(公式)
事象Aが起こった時に、事象Bが起こる条件付き確率$P_{ A }(B)$は
$P_{ A }(B)=\dfrac{P(A∩B)}{P(A)}$
但し$P(A)$はAの起こる確率、$P(A∩B)$はAとBが同時に起こる確率
$P(A∩B)$は先ほどの補足で求めた確率です。
これを使って先ほどの問の(2)を解くと
$P_{ A }(B)=\dfrac{\dfrac{7}{20}}{\dfrac{1}{2}}=\dfrac{7}{10}$
となり先ほどの答えと一致します。
(事象Aを奇数の人を選ぶ、事象Bを英語が好きな人を選ぶとしています)
この公式と条件付き確率のイメージがどちらも使いこなせるとどんな問題でも解けるようになります。
まずは簡単な例からイメージをしっかり掴んでいってください。
******************************
全国対応!高校数学・物理化学専門の
オンライン家庭教師・個別指導学習塾、
栃木県宇都宮市近辺の家庭教師を
お探しならこちらをクリック
↓ ↓ ↓