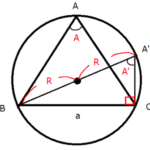
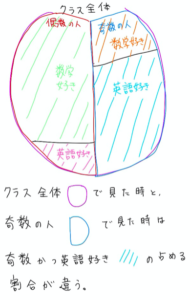
【数学１】図形と計量①／三角比（sin、cos、tan）とは？その２通りの求め方

数学１で学ぶ「図形と計量」では、中学の数学で学んだ「図形」の知識を発展させて、図形の性質を利用して論理的に物事を考え、普段の生活でも問題解決に役立てられるようになることを目標にしています。

今回は「三角比」について説明していきます。

三角比は「図形と計量」の根幹となる部分であり、社会に出てからも測量や設計、プログラミングなど、様々な場面で必須となる知識です。

これを機会にしっかり理解しておきましょう。

中学までに勉強した数学の内容も出てきますが、その都度復習しますので、安心してくださいね。

１，三角比、sin、cos、tanとは？

三角比について説明する前に、三角形について小中学校の数学で学んだ内容を復習しましょう。

以下の（　）に入る言葉を考えてみてください。
① 三角形の内角の和は（　 ）度である。
② １つの内角が90度の三角形を
（　　　　）三角形という。

どうでしょうか？簡単すぎたかもしれませんね。

答えは、①が180°、②が直角です。

この直角三角形の各辺の長さの比のことを三角比といいます。

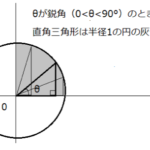
例えば下の三角形の図を見てください。

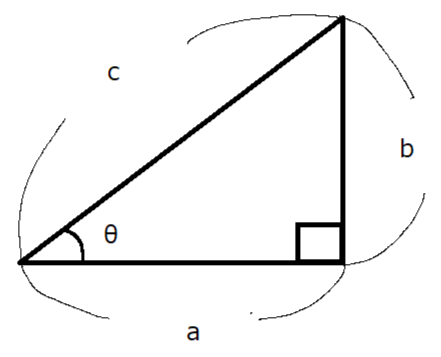
各辺をa、b、cとして、90度ではない2つの角度のうち１つをθとします。

θは三角比で角度を表すときに使われることが多いギリシャ文字で、読み方は「シータ」と言います。

三角形の内角の和は180度で、θともう1つの角度の和が90°なので
0° < θ < 90°になります。

90°よりも小さな角度のことを鋭角、
90°よりも大きな角度のことを鈍角と言いましたよね。

なので、θは鋭角ということになります。

この時、辺a、b、cの比を以下のように表します。

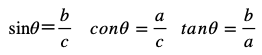
sinは、sineの略で、「サイン・シータ」と読み、日本語では「正弦（せいげん）」と言います。

cosはcosineの略で「コサイン・シータ」と読み、日本語では「余弦（よげん）」と言います。

tanはtangentの略で「タンジェント・シータ」と読み、日本語では「正接（せいせつ）」と言います。

そして、このsinθ、cosθ、tanθ をまとめて「三角比」と言います。

2、三角比の覚え方①

「これ暗記するの？　分かりにくい……」という場合は、次のように覚えましょう。

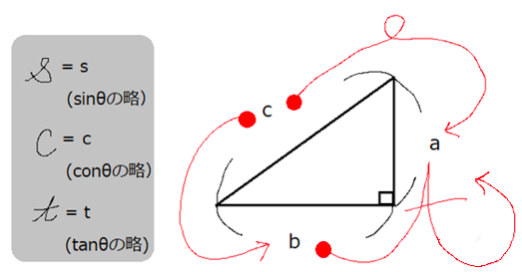
上の図を見てください。
●からスタートして矢印の方向に向かって、英語の筆記体が書かれています。

●のある辺を分母、矢印の指す辺が分子と考えてください。

英語の筆記体に馴染みのない時のために、アルファベットのどの文字に該当するかも左図に示しておきました。

アルファベットの頭文字が、三角比の頭文字と一致するので覚えやすいと思います。

３、三角比の覚え方②

先程の覚え方では筆記体に馴染みがないとかの理由で、三角比覚えられないという場合は、次のような覚え方もあります。

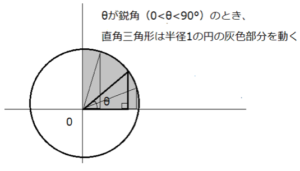
xy平面上に半径1の円があり、その中に直角三角形があると考えてください。

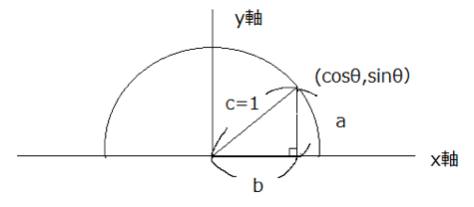
この場合

となり、直角三角形が円と接している点のyの値、つまり直角三角形の高さがsinθであることが分かります。同様に、

となり、直角三角形が円と接している点のxの値、つまり直角三角形の底辺の長さがcosθであることが分かります。

以上より、xy平面上の点で表すと、(x,y)=(cosθ,sinθ)となります。

次に、同じくxy平面上に、半径1の円があり、直角三角形の底辺bが1で円に接していると考えてください。

先ほどは一番長い斜辺cを１としましたが、今度は底辺bを1にしたところに注意してくださいね。

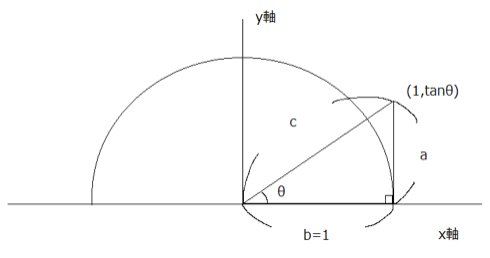
この場合、

となり、三角形のx軸と接していない頂点のyの値、つまり直角三角形の高さがtanθであることが分かります。

４、三角比に関する問題

それでは実際に三角比に関する問題を解いてみましょう。

中学の数学で習った内容も出てくるので、復習もかねて挑戦してみてください。

＜問題＞
次の図の直角三角形ABCにおいて、
sinA、cosA、tanA値を求めよ。

---

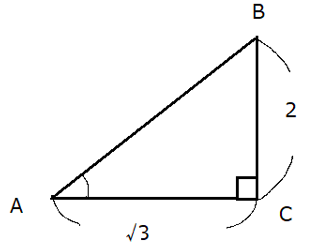
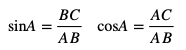
なので、まずは辺ABの長さを求める必要があります。

三平方の定理より

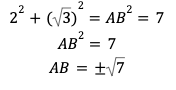
AB>0より、AB=7となります。よって

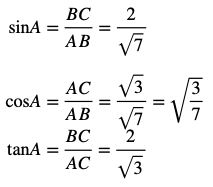
いかがでしたか？

中学校で勉強した三平方の定理も三角比の求め方も、ポイントを押さえていればそれほど難しくないですよね。

基礎の考え方を押さえておけば、公式を忘れてしまっても自分で導き出せるようになるので、しっかり理解をしておきましょう。

******************************
全国対応！高校数学・物理化学専門の
オンライン家庭教師・個別指導学習塾、
栃木県宇都宮市近辺の家庭教師を
お探しならこちらをクリック
↓　↓　↓