【数学A】場合の数と確率②場合の数の求め方(樹形図、積の法則、和の法則)


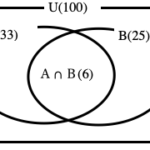
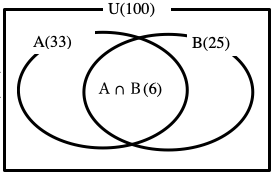
【数学A】場合の数と確率①/集合の要素の個数とベン図・個数定理による求め方からの続き
今回は、「樹形図」「積の法則」「和の法則」を使った場合の数の求め方を学習します。
場合の数とは何パターンあるかという意味です。
全てのパターンを漏れなく、重複することなく、いくつのパターンがあるかを求めます。
場合の数を求める時に役に立つのが「樹形図」 「積の法則」「和の法則」です。
1、樹形図による場合の数の求め方
![]()
6枚のカードを並べて3 桁の数を作ります。
全部で何通りあるか。
【解答】
この問題は樹形図を使って場合の数を見つけましょう。
樹形図を作ると下図のようになります。
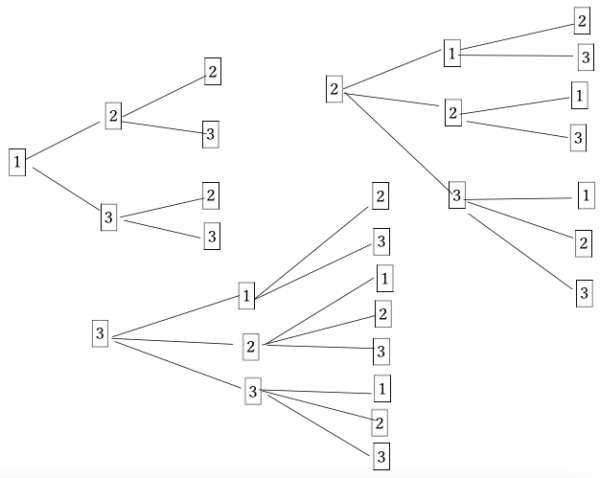
枝分かれのパターンを数えます。
この場合19パターンで、
答えは「19通り」です。
この樹形図を作る際に
![]()
使えるカードの枚数が違っていることに気をつけましょう。
2、和の法則による場合の数の求め方

【例題】(2)大小2つのサイコロを投げる時、目の和が6または、7になる場合は何通りあるか。
(解答)
大きいのサイコロの目をa、
小さいのサイコロの目をbとする。
①目の和が6になる場合は
(a, b)=(1,5)(2,4)(3,3)(4,2)(5,1)
となるので5通りあります。
②目の和が7になる場合は
(a, b)=(1,6)(2,5)(3,4)(4,3)(5,2)(6,1)
となるので6通りあります。
①と②の起こり方に重複はないから和の法則を使って、5+6=11となり答えは「11通り」
3、積の法則による場合の数の求め方

【例題】(3)次の整数の正の約数は全部で何個あるか。
①24 ②360
(解答)
【①の解答】24の約数は数が小さいので、全部挙げてもできます。
(1,2,3,4,6,8,12,24)で
24の正の約数の個数は8個です。
素因数分解による約数の個数の求め方
②の360の約数の個数を求める時には、場合の数が多いので、樹形図を使わないほうがいいでしょう。
これは素因数分解を使って、約数の個数を求めます。
24を例にして考えていきましょう。
24を素因数分解すると、
24=23✕3です。
下のような筆算で求める事が多いです。
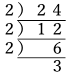
正の約数は、
A={1,2,22 ,23 }の4通りと
B={1,3}の2通りの中から1つずつ選び
それらをかけ合わせると
24の正の約数になります。
小さい数なら樹形図を使ってもできます。
下の樹形図も参考にして考えてみましょう。

樹形図からも分かるように、積の法則を使うと簡単にできます。
A の場合の数が4通りです。
B の場合の数が 2通りです。
だから、積の法則より正の約数の数は、4×2=8 答は8通りです。
ところで素因数分解 24=23×3 で
2の指数は3でAの個数 4個
3の指数は1でBの個数は2個になっています。
一般的に正の整数を素因数分解して、それぞれの素数の指数に1を足した数を、すべて掛け合わせた数が正の約数の個数となります。
正の約数の問題はテストなどでよく出るので、次のように覚えておくと便利です。

【②の解答】
360を素因数分解すると、
360=23×32×5 です。
2の指数は3、3の指数は2、5の指数は1なので
(3+1)×(2+1)×(1+1)=4×3×2=24
となり答え 24通り です。
3、まとめ
場合の数を求めるのに、「樹形図」を作ることが出来れば数える事で求めることができます。
「万能です。」と言いたいところですが、場合の数が少ないときは良くても、多いと樹形図を書くのが大変です。
だから、いつも使えるとは限りません。
「積の法則」は「AかつB」の関係の時に使います。
「和の法則」は「AまたはB」の関係の時に使いますが、「和の法則」の時はAとBで重複が無いことが条件 です。
次回は順列について学習します。
******************************
全国対応!高校数学・物理化学専門の
オンライン家庭教師・個別指導学習塾、
栃木県宇都宮市近辺の家庭教師を
お探しならこちらをクリック
↓ ↓ ↓