【数学A】場合の数と確率③順列とは?「!」、「P」の公式と活用問題


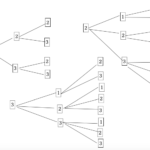
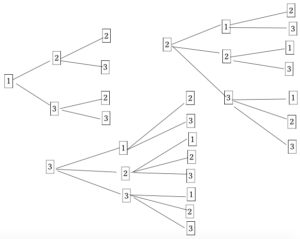
【数学A】場合の数と確率②場合の数の求め方(樹形図、積の法則、和の法則)からの続き
今回は「順列」について解説します。
「順列」とは、順番に1列に並べることです。
順列を理解できれば並べ方の場合の数を求めることができるようになります。
1、「nPr」「!」とは?順列に関する記号と公式
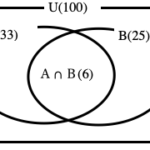
異なるn個からr個取りだして順番に並べる場合の数を、n個からr個取る順列と言います。
n個からr個取る順列の総数は
nPrと表します。

またn個全部を順に並べるときの場合の数は
n(n-1)(n-2)・・・3×2×1 となり、
これをn!と表します。
(nの階乗と言います。)
![]()
では例題でその使い方を見ていきましょう。
【例題1】(1)6!を求めよ。(2)7P3 を求めよ。
(解答)
(1)6!=6×5×4×3×2×1=720
(2)7P3 =7✕6✕5=210
(7からカウントダウンして3個かける)
【例題2】a,b,c,d,e,f,g,hの8個の数から4個取り出して順番に並べるとき、並べ方は何通りあるか。
(解答)
8個の中から4個選んで並べる並べ方なので
8P4 =8×7×6×5=1680
答え 1680通り
【例題3】1、2,3,4の4個の数字を並べて4桁の整数を作る。この時奇数となるものは何通りあるか。
(解説)
まず奇数となるためには、1の位の数が1または3になる必要があり、その場合の数は2通り。
千の位、百の位、十 の位には1の位の数を除いた残り3個の数を並べると考えて、3!=3×2×1=6 の6通り。
したがって求める場合の数は
3!✕2=6✕2=12
答え 12通り
2、隣り合う並び方、隣り合わない並べ方
次に特定の人が隣り合う並べ方の問題です。
この問題を解くにはちょっとしたアイデアが必要です。
【例題4】女子5人、男子3人が1列に並ぶとき、次のような並び方は何通りあるか。
(1)男子3人が皆隣り合う
(2)男子同士が隣り合わない。
(1)
男子3人をひとまとめにして1組にします。
女子5人と男子1組を並べ る場合の数は
6!=6×5×4×3×2×1=720通り

![]()
この720通りのそれぞれに対して隣り合う男子3人の並び方は3!=3×2×1=6通り
したがって求める並び方の場合の数は
6!✕3!=720×6=4320
答え 4320通り
(2)
下図のように女子5人を並べて、その間と両端に男子3人を1 人ずつ並べると考える。
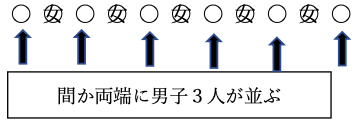
まず、女子5人の並び方は、
5!=5×4×3×2×1=120
となるので120通り。
次に女子と女子の間または両端の6ヶ所に男子3人が並ぶ場合の数を求める。
6個の〇から3ヶ所選んで、その中で男子3人が並ぶと考える。
6個の中から3個選んで順番に並べることになるので、
6P3 =6✕5✕4=120通り
したがって求める場合の数は
5!✕6P3
=120✕120
=14400
答え14400通り
順列には、色々なパターンの問題があります。
それぞれに解き方のアイデアがあります。
次回も「順列」を学習します。
また別のパターンを見ていきましょう。
******************************
全国対応!高校数学・物理化学専門の
オンライン家庭教師・個別指導学習塾、
栃木県宇都宮市近辺の家庭教師を
お探しならこちらをクリック
↓ ↓ ↓