【数学A】場合の数と確率④順列(0を含む数字の並べ方、色分けの数)


【数学A】場合の数と確率③順列とは?「!」、「P」の公式と活用問題からの続き
「順列」については、色々な条件が付く問題があります。
今回はその中から「数字の問題」と「色分けの問題」を取り上げます。
1、整数の個数(0を含む数字を並べる)
【例題1】0,1,2,3,4の5つの数から、重複しないで3個の数を並べて3桁の正の整数を作る。
このとき次のような整数は何個作れるか。
①3桁の正の整数すべて
②偶数になるもの
③3の倍数になるもの
①(解答)
数字の問題は前回も学習しましたが、今回の問題は、選択する数字に0が含まれています。
・1番上の百の位には0が使えないので
百の位は1,2,3,4の4通り。
・残り4個の数の中から2個選び、十の位と一の位に並べるので十の位と一の位の場合の数は
4P2=4×3=12通り
したがって求める3桁の整数の個数は
4×12=48
答え 48個
①の(別解)
5つの数から、重複しないで
3個の数を並べる場合の数から
百の位が0になる場合の数を引きます。
5P3―4P2
=5×4×3―4×3
=60―12
=48
②(解答)
偶数は一の位が、0,2,4の場合。
百の位は0ではいけないので、場合分けする。
・一の位が0のとき
百の位と十の位は残りの4つの数 1,2,3,4のから2個選んで並べるので、
4P2=4×3=12通り
・一の位が0でないとき
一の位は、2または4の2通り
百の位は0以外だから1,2,3,4の4通りから一の位で使った数を取ると3通り。
十の位は残りの2個の数に0を加えた3個の数から選ぶので3通り。
したがって2×3×3=18通り。
よって求める数は
12+18=30
答え 30個
③(解答)
各位の数の和が3の倍数になる時、その数は3の倍数になる。
0,1,2,3,4の中で3個の数の和が3の倍数になる組合せは、
{0,1,2} {0,2,4}
{1,2,3} {2,3,4}の4通り。
これを0を含むものと、0を含まないものとに場合分けする。
・{0,1,2} {0,2,4}のとき
{0,1,2} のとき
百の位は0ではないので
2×2!=4 となり4通り。
{0,2,4}のとき同様にして
2×2!=4 となり4通り。
・{1,2,3} {2,3,4}のとき
{1,2,3}のとき
3!=3×2×1=6 となり、6通り。
{2,3,4}のときも同様にして6通り。
求める数は、これらをたして、
4+4+6+6=20
答え 20通り
2、色分け
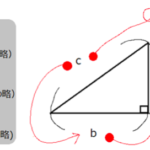
次は色分けの問題です。図をよく見て考えてください。
【例題2】
下の図でA,B,C,Dを赤、青、白、黒の4色で塗り分けるとき、次の塗り分け方は何通りあるか。
①4か所をすべて異なる色で塗る場合
②同じ色を使ってもよいが隣り合う部分は異なる色にする場合
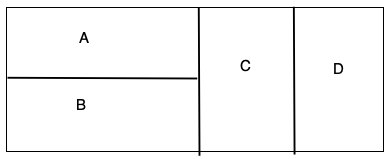
(解答)
①4個を1列に並べる事と同じなので、その塗り分け方は
4!=4×3×2×1=24
答え24通り
②AとBとCは隣り合うので、同じ色にはならない。
A,BとDは隣り合わないので同じ色でも、違う色でも良い。
よって塗り分ける色の数は、4色の場合と3色の場合がある。
(4色の場合)
①と同じだから24通り
(3色の場合)
AとDが同じ色とすると、A,B,Cの色は4色の中から3色選んで当てはめるので
4P3=4×3×2=24通り
BとDが同じ色のときも
同様にして24通り
この2つの起こり方は
重複しない(同時には起こらない)ので
24+24=48通り
したがって求める数は、
4色の場合と3色の場合を合わせて
24+48=72通り
答え 72通り
3、まとめ
「数字の問題」では0がある場合と0がない場合では解き方が異なります。
「色分けの問題」では、図を見て場合分けをしましょう。
******************************
全国対応!高校数学・物理化学専門の
オンライン家庭教師・個別指導学習塾、
栃木県宇都宮市近辺の家庭教師を
お探しならこちらをクリック
↓ ↓ ↓