【数学A】場合の数と確率⑤円順列、数珠順列、正多面体の塗り分けの数


【数学A】場合の数と確率④順列(0を含む数字の並べ方、色分けの数)からの続き
今回は「円順列」とその応用の「数珠順列」、「正多面体の塗分け」について説明します。
まず円順列がこれらの問題を解くための基本となります。
1、円順列
【例題1】
1番~6番までの番号が付いた
6人の生徒が丸いテーブルに座る。
このとき次のような並び方は何通りあるか。
①6人の並び方
②1番と2番の生徒が隣り合う
③1番と2番の生徒が隣り合わない
①(解答)
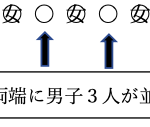
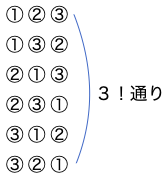
下の図は6人に番号を付けて円形に並べたものです。
まず前提として上の図のように円形に座るとき、位置は違いますが並び方の順番が同じです。
この場合は同じなので、6通り重複しているとみなします。
このように円形に並べる順列を円順列といいます。
1列に並ぶ順列ならば、6!ですが、そのそれぞれに重複が6通りあるので、このときの並べ方の数は
6!÷6
=(6✕5✕4✕3✕2✕1)÷6
=120通り
答え 120通り
一般的に円順列については次のように求められます。

②(解答)
1番と2番をまとめて1組と考えます。
この1組と残りの他の4人の並び方は
(5-1)!
=4!
=4×3×2×1
=24 となるので、
24通り。
次に1番と2番の2人を
1組の中で動かすと並び方は
2!=2×1=2通り
よって求める並べ方は
2×24=48
答え 48通り
③(解答)
1番と2番が隣り合わない並び方の数は、②の1番と2番が隣り合う並び方の数を、①の全体の並び方の数から引くと求められます。
したがって
120-48=72より
答え 72通り
2、数珠順列
次に円順列の応用の「数珠順列」の問題です。
【例題2】
赤、青、黄、黒、白 の5色の玉をつないで首飾りを作る。
玉の並べ方は何通りあるか。
(解答)
この問題は円順列の応用問題です。
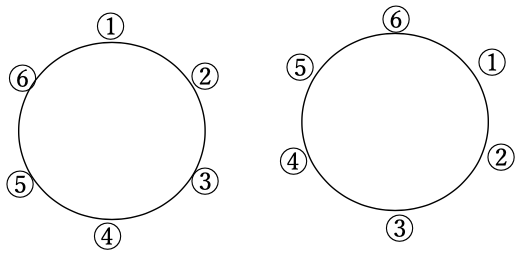
テーブルの問題との違いは、下図を見てください。
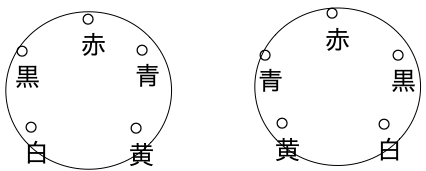
首飾りは裏返す事ができ、裏返して同じになるものは重複していると考えます。
だから5個の円順列を半分にすれば求める並べ方の数がわかります。
よって
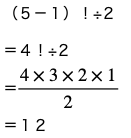
答え 12通り
このような順列を数珠順列といいます。
まとめると

3、正多面体の塗り分け
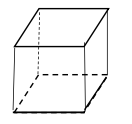
最後に有名な正多面体の塗り分け問題です。今回は正六面体です。
【例題3】
下の図のような正六面体を次の条件で塗り分ける。ただし隣り合う面は同色にしない。
また、回転させて一致する塗り方は同じとみなす。
①異なる6色で塗り分ける場合何通りあるか
②異なる5色で塗り分ける場合何通りあるか
(解答)
正多面体の塗り分けの問題は、ある面を固定すると円順列や数珠順列の考え方が利用できる。
①(解答)
このような問題は、底面を1色に固定することで求められる。
底面を1色固定すると上の面の色は5通り。
そのそれぞれに対して、側面の色は4色の円順列となるので
(4-1)!=3!=3×2×1=6通り。
したがって求める色の塗り方は
5×6=30通り
答え 30通り
②(解答)
底面と上の面を同色で固定します。
この2つの面の選び方は5通り。
底面と上面は裏返しても同じなので、側面の色の並び方は4個の数珠順列となる。
よって側面の色の塗り方は
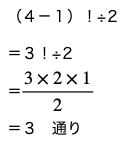
したがって求める色の塗り方は
5×3=15通り
答え 15通り
今回は説明した「円順列」についての問題は色々なパターン があります。
どの解き方のパターンが使えるか見極めましょう。
******************************
全国対応!高校数学・物理化学専門の
オンライン家庭教師・個別指導学習塾、
栃木県宇都宮市近辺の家庭教師を
お探しならこちらをクリック
↓ ↓ ↓