【数学A】場合の数と確率⑥組合せの記号「C」とその公式、計算方法


【数学A】場合の数と確率⑤円順列、数珠順列、正多面体の塗り分けの数 からの続き
ここでは「組合せC」の公式とその計算方法について触れていきます。
「順列」では取りだして並べた場合の数を求めていました。
一方「組合せ」では順番を無視した取り出し方の場合の数を求めます。
組合せの記号「C」と公式
異なるn個から、異なるr個を取る「組合せ」の総数を nCr (r≦n)と表 します。
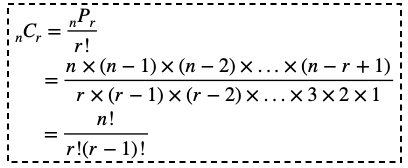
異なるn個の中から異なるr個を取り出して並べる順列はnPrです。
順列では取り出したr個の並べる順番が違っていたら別のものとします。
この場合の数はr!通りあります。
「組合せ」では、取り出したr個は並べる順番は無視します。
よってr!通りの重複があると考えますので、組合せnCrはnPrを重複の場合の数r!で割ることで求められます。
少し分かりにくいので、具体例で見ていきましょう。
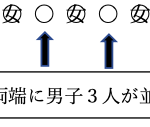
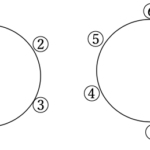
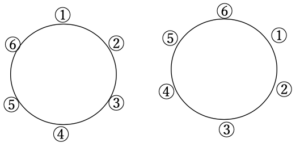
①②③④⑤⑥から3個取り出して並べるとすると、その並べ方は6P3=120通りあります。
下図のように①②③を選んで並べた時、その3つの並べ方は3!=6通りです。
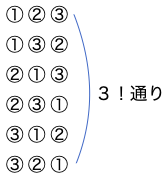
組合せでは順番を無視するので、これらは同じものとなります。
だからこの6通りは重複します。
①②③以外を選んだ時も、同じように重複するので、
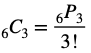
が成り立ちます。
このようにして一般的に
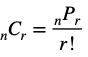
が成り立つのです。
また
nPr=n(n−1)(n−2)・・・(n−r+1)
r!=r(r-1)(r-2)・・・3×2×1
を代入すると
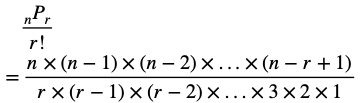
となります。
さらに
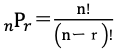
を代入して、分母分子に
(nーr)!を掛けると
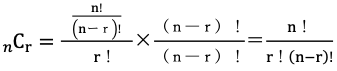
となります。
組合せの計算
【例題1】
次の値を求めよ。
①7C2 ②7C5
(解答)
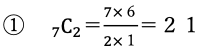
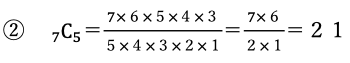
①と②の答えが等しくなっています。
一般的に次のことが成り立ちます。
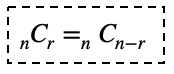
では具体的な内容の文章問題を解いてみましょう。
【例題2】
10色の色鉛筆の中から4色選ぶ方法は何通りあるか。
(解答)
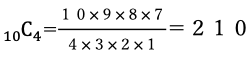
答え 210通り
次の問題は男女の混じった集団から、色々な条件を付けた組合せを求める問題です。
【例題3】
男子5人と女子4人の中から4人を選ぶとき、次のような選び方は、それぞれ何通りあるか。
①すべての選び方
②男子3人と女子1人を選ぶ選び方
③少なくとも1人は女子を選ぶ選び方
④特定の2人を選ぶ選び方
(解答)
①9人の中から4人を選ぶので
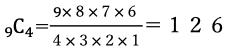
答え 126通り
②男子5人の中から3人を選び、
かつ女子4人の中から1人を選ぶ。
この2つの場合の数を掛ければ求める数が得られる。

③少なくとも1人とは、女子が4人、3人、2人、1人いずれでも良い。
場合分けをして求める事もでるが、4人とも男子を選ぶ以外と考えると、全部の場合の数から4人とも男子の場合の数を引くと求める事ができる。
よって
126ー5C4
=126ー5C1
=126ー5
=121
答え 121通り
④2人が選ばれるのは決定しているので、残り7人の中から2人を選ぶと考える。
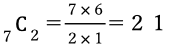
答え 21通り
今回は「組合せ」の基本的な記号といくつかの問題を説明しました。
「組合せ」の問題は色々なパターンがありますので、次回も引き続き見ていきましょう。
******************************
全国対応!高校数学・物理化学専門の
オンライン家庭教師・個別指導学習塾、
栃木県宇都宮市近辺の家庭教師を
お探しならこちらをクリック
↓ ↓ ↓