【数学A】場合の数と確率⑦組合せの図形への利用、順列と組合せの使い分け


【数学A】場合の数と確率⑥組合せの記号「C」とその公式、計算方法 からの続き
「組合せ」の問題には色々なパターンがあります。
今回は「組分け」、「図形への利用」、「順列と組合せの使い分け」の問題について解説します。
組分けの問題
【例題1】12人を次のように分ける方法は何通りあるか。
①5人,4人,3人の3組に分ける。
②4人ずつA,B,Cの3組に分ける。
③4人ずつ3組に分ける。
④6人,3人,3人の3組に分ける。
(解答)①
・12人から5人を選ぶ場合の数は
12C5通り
・残りの7人から4人選ぶ場合の数は
7C4通り
残りの3人は自動的に決まるので、求める場合の数は
12C5✕7C4
=792✕35
=27720
答え 27720通り
②
・Aに入る4人を選ぶ場合の数は
12C4通り
・Bに入る4人を残り8人から選ぶ場合の数は
8C4通り
12C4✕8C4
=495✕70
=34650
答え 34650通り
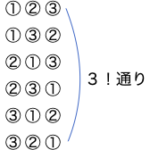
③A、B、Cの区別をなくすと同じ選び方が下図のように3!通りできる。
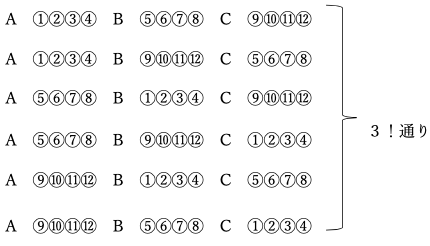
つまり②の34650通りの中で3!=6通りずつ重複ができるので、求める場合の数は34650÷6=5775
答え 5775通り
④Aに6人、B に3人、C に3人を選ぶ場合の数は
12C6✕6C3
=924✕20
=18480
BとCの区別をなくすと同じ分け方が2通り(2!通り)ずつ重複するので、求める数は
18480÷2=9240
答え 9240通り
組合せを図形に利用
次に組合せを使う図形の問題を見てみましょう。
【例題2】
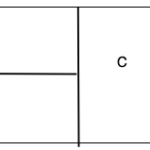
下図のように、縦4cm横4cmの正方形がある。
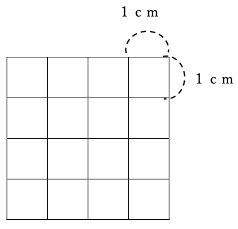
この正方形を縦横とも1cm幅に分けて、図のように縦1cm、横1cmの正方形にする。
①長方形は(正方形を含む)は全部で何個できるか。
②正方形は全部で何個できるか。
(解答)
①長方形は縦と横2本ずつの直線の組合せで作ることができる。
縦、横どちらも5C2通りあるので、求める長方形の数は
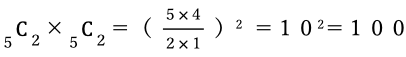
答え 100個
② 正方形は1辺の長さで場合分けする。
(ⅰ)1辺1cmの正方形は隣り合う縦横とも2本の直線の組合せでできる。
5本の直線から隣り合う2本の直線の組合せは縦横4通りずつあるので、求める正方形の数は
4×4=16通り
(ⅱ)1辺2cmの正方形は縦横とも2cm離れた2本の直線の組合せでできる。
組合せは縦横とも3組ずつあるので3×3=9通り
(ⅲ)1辺3cmの正方形は縦横とも3cm離れた2本の直線の組合せでできる。
組合せは縦横とも2組ずつなので
2×2=4通り
(ⅳ)1辺4cmの正方形は上の図の全体の正方形だから1組。
(ⅰ)〜(ⅳ)より求める正方形の個数は16+9+4+1=30
答え 30個
順列と組合せの使い分け
【例題3】
①10人の生徒から3人を選ぶ選び方は何通りあるか。
②10人の生徒から3人を選び、委員長と副委員長と書記を選ぶ選び方は何通りあるか。
③赤玉4個と白玉6個の10個の玉を並べる並べ方は何通りあるか。
(解答)
①は「組合せ」で解く。
10人の生徒から3人を選ぶので
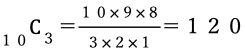
②「選ぶ」「選び方は何通りありますか。」など組合せを思わせる言葉が出てくるが、これは順列で解く。
取り出すだけでなく区別する。
区別するのは並べる事と同じ扱いと考えます。
10P3=10✕9✕8=720
答え 720通り
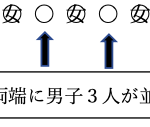
③下図のように並べた10個の玉のうち、赤にする玉を10か所から4か所選ぶと考えられる。(並べるので順列とも考えられる)

したがって10C4で求められる。
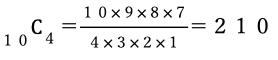
答え 210通り
今回は組合せの色々なパターンの問題を学習しました。
例題3は「同じものを含む順列」の問題と考えると別解があります。
次回はその「同じものを含む順列」についてお伝えします。