【数学A】場合の数と確率①/集合の要素の個数とベン図・個数定理による求め方


数Ⅰで「集合」について勉強しましたが、今回お伝えする「場合の数」でも「集合」を使うので、まずはその復習から始めます。
「集合」では、独特の記号や表現が使われましたが、ここでは集合の要素の個数の表し方から始めていきます。
まず、最初に次の表し方を覚えましょう。
1、集合の個数の表し方
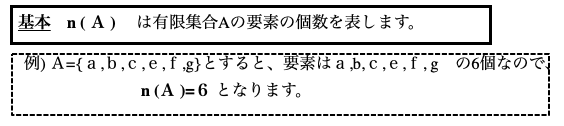
【例題】(1)
全体集合を
U={1,2,3,4,5,6,7,8,9}とする。
Uの部分集合
A={2,3,5,6,7}
B={1,3,6,7}について
![]()
(解説 解答)
➀n(A)については、
A={2,3,5,6,7,}だから
Aの要素は、2,3,5,6,7の5個。
答えn ( A )= 5
②n(B) については
B={1,3,6,7}だから
Bの要素は、1,3,6,7の4個。
答えn ( B)=4

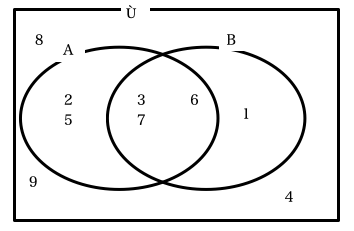
③や④のような問題を考える時は、上のような図を使って考えるのがいいと思います。
(このような図をベン図といいます。)
2、個数定理
では、次に下の式が成り立つことを上のベン図を見ながら確かめてください。
そして、これは基本の式として覚えておきましょう。

【例題】(2)
全体集合をU。AとBはUの部分集合とする。
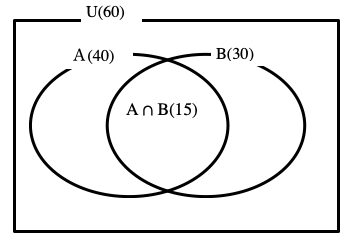
n(U)=60,n(A)=40,n(B)=30,n(A B)=15の時、次の集合の要素の個数を求めよ。
![]()
(解説 解答)
この問題では、各集合の要素が具体的に示されていません。
そこで、次のような図を書いて考えることをお勧めします。

【例題】(3) 100以下の自然数について
①3または4の倍数となる自然数はいくつあるか。
②3の倍数ではない自然数はいくつあるか。
③3の倍数でも4の倍数でもない自然数はいくつあるか。
(解説 解答)
分かりやすくするために次の集合を考えます。
U={1から100までの自然数}
A={3の倍数(1から100までの自然数の中で)}
B={4の倍数(1から100までの自然数の中で)}
ベン図を書くと下図のようになります。
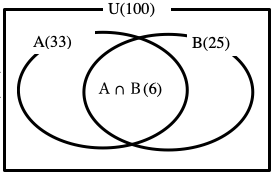
n(A)は次のように求めます。
A={3×1,3×2,・・・,3×33}だから
n(A)=33
同じようにして
B={4×1,4×2,・・・,4×25}だから
n(B)=25
次に1から100までの自然数の中の、3と4の最小公倍数12の個数を求めます。
A∩B ={12×1,12×2,・・・,12×8}
よってn(A∩B)=8

3、3つの集合の場合の数
【例題】1から100までの自然数のうち2または3または5の倍数は何個ありますか。
(解説 解答)
2または3または5の倍数というのは、2の倍数でも3の倍数でも5の倍数のどれでもよいという事です。
Uを全体集合。、の部分集合をA , B , C として下のように集合を定義します。(「定義します」とは、このように決めますという意味です。)
U={n|nは1から100までの自然数}
A={n|nは2の倍数}
B={n|nは3の倍数}
C={n|nは5の倍数}
Uは全体集合です。
A , B , CはUの部分集合なので、(1から100までの自然数の中で)という条件がついています。
求めたい集合の数はn(A ∪ B ∪C)です。
まず部分集合A , B , Cの個数を求めます。
100以下の2の倍数は100÷2=50から50個と簡単に見つけられます。
3の倍数についても100÷3=33余り1より33個とわかります。(余りは気にしなくて大丈夫です)
5の倍数についても100÷5=20から、
20個です。
次に部分集合A , B , Cの共通部分A∩B、B∩C、A∩C、A∩B∩Cの個数を求めます。
A∩Bは、2と3の最小公倍数6の倍数です。
全体集合は、100以下の自然数なので、
100÷6=16余り4より
n(A∩B)=16
B∩Cは、3と5の最小公倍数15の倍数なので、100÷15=6余り10より
n(B∩C)=6
A∩Cは、2と5の最小公倍数10の倍数なので100÷10=10より
n(A∩C)=10
A∩B∩Cは、2と3と5の最小公倍数30の倍数なので100÷30=3余り10より
n(A∩B∩C)=3
まとめると
①n(A)=50
②n(B)=33
③n(C)=20
④n(A∩B)=16
⑤n(B∩C)=6
⑥n(A∩C)=10
⑦n(A∩B∩C)=3
今、求めたい2または3または5の倍数の個数はn(A∪B∪C)ですが、ここで個数定理の拡張定理を使います。
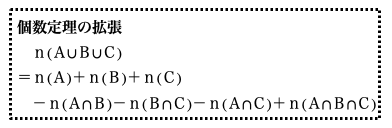
こうなる理由は後で説明します。
この公式に準備した①~⑦の数値を代入して答えを導きだします。
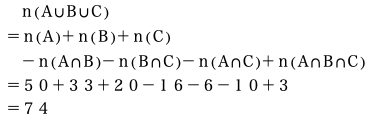
答え74個
4、個数定理の拡張の理由
個数定理の拡張を説明する前に下のベン図を見てください。
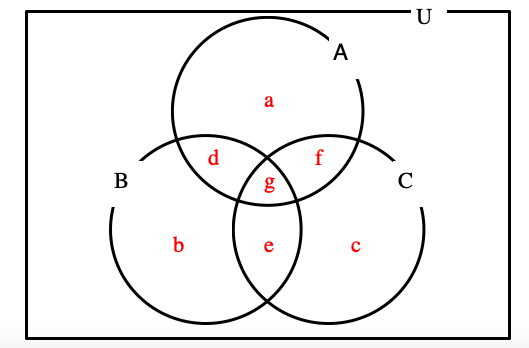
全体集合をU とします。A , B , CはUの部分集合です。
a~gは各部分の要素の個数を表します。
![]()
これはベン図を見たら分かります。
次に個数定理の拡張の右辺をa~gを使って表してみます。
まず準備として
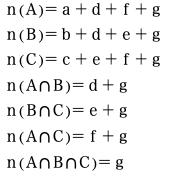
これを個数定理の拡張の右辺に代入します。
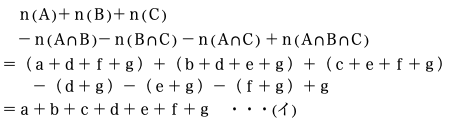
(ア)と(イ)の右辺が一致するので個数定理の拡張が成り立ちます。
******************************
全国対応!高校数学・物理化学専門の
オンライン家庭教師・個別指導学習塾、
栃木県宇都宮市近辺の家庭教師を
お探しならこちらをクリック
↓ ↓ ↓