【数学A】場合の数と確率⑧同じものを含む順列と重複組合せによる並べ方


【数学A】場合の数と確率⑦組合せの図形への利用、順列と組合せの使い分け からの続き
前回まで「順列」と「組合せ」について説明してきましたが、今回は「同じものを含む順列」と「重複組合せ」についてです。
同じものを含む順列
【例題1】
赤玉4個と白玉6個の10個の玉を並べる並べ方は何通りあるか。
(解答)
まずは10個の玉の順列と考えます。
10個を並べる場合の数は10!通りです。
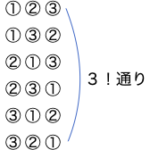
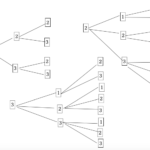
下図のようにこの色の並び方の中で赤玉に番号をつけてみると、赤玉を動かす場合の数は、4!通りです。

赤玉は区別できないのでこれらは重複します。
白玉も同じ様にして重複していると考えると白玉の重複は6!通りなので、求める場合の数は重複している分を割って求めることができます。
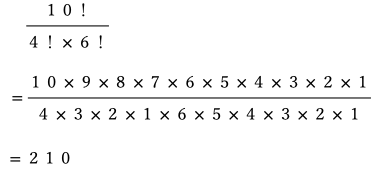
答え 210通り
一般的に同じ「同じものを含む順列」の総数については次の通りです。

上の公式を使って解く練習をしましょう。
【例題2】
8個の数字1,1,1,2,2,2,3,3の全部を使って8桁の整数を作るとき何個の整数が作れるか。
(解答)
1が3個、2が3個、3が2個、同じものを含む順列だから求める場合の数は
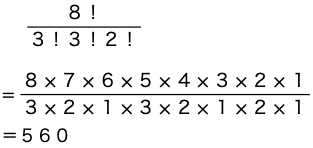
答え 560通り
重複組合せ
次に重複組合せについて説明します。
同じものを含む順列の考え方を利用します。
実際に問題を見ながら説明していきましょう。
【例題3】
1,2,3の3個の数から重複を許して6個の数を取り出す。ただし含まれない数があっても良い。このとき取り出し方は何通りあるか。
(解答)
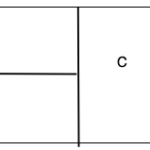
例えば1を2個、2を3個、3を1個取り出すとする。
下図のように、1を2個、2を3個、3を1個並べて、間に仕切りの縦線を1つ入れると考える。
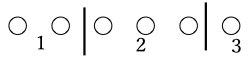
また1が4個、2が0個、3が2個のように、含まれない数がある場合は、下図のように区切りが連続で入ると考えます。
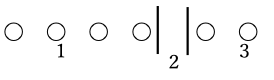
さらに1が2個、2が4個、3が0個の場合は、下図のように仕切りを右端に置くと考えます。
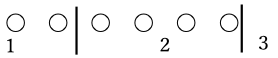
このように、重複を許して6個の〇と2個の仕切りと合わせて8個1列に並べることにと同じとみなせます。
だから求める場合の数は「同じものを含む順列」と考えられ、次のようになります。
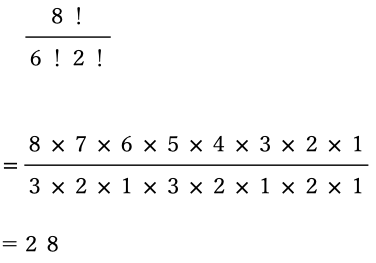
答え 28通り
(別解)
仕切りを置く場所を8か所から2か所選ぶことと同じだから、求める数は
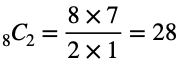
となります。
〇の方を6か所選ぶと考えれば 8C6ですが、8C2=8C6で計算が楽なので、こちらがいいと思います。
一般的に次のことが成り立ちます。
異なるn個の中から重複を許してr個取るとき、仕切りの数は(n―1)個となる。

今回は「同じものを含む順列」と「重複組合せ」について扱いましたが、色々なパターンの問題があります。
どのパターンの問題かを見極めて、使い分けできるようにしましょう。
******************************
全国対応!高校数学・物理化学専門の
オンライン家庭教師・個別指導学習塾、
栃木県宇都宮市近辺の家庭教師を
お探しならこちらをクリック
↓ ↓ ↓