二次不等式の図による解き方/絶対値が付く二次関数のグラフの書き方
二次方程式解き方と解の公式、判別式と二次関数の共有点の個数の関係 からの続き 二次不等式とは、多項式の最も大きい次数が二次式になっている不等式です。 例えばx2+x+1≦0というのは二次不等式です。 ax2+bx+c≦0 […]
二次方程式解き方と解の公式、判別式と二次関数の共有点の個数の関係
中学生の時に学習したように、 二次方程式とは、 ax2+bx+c=0 の形をした式のことでした。 (a,b,cはそれぞれ実数でa≠0) 二次方程式は基本的に 次のいずれかの方法をとることによって 解くことが出来ます。 ① […]
二次関数の最大値・最小値/関数が固定されて区間(定義域)が動く場合
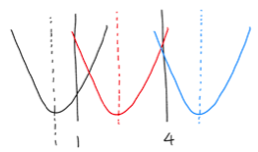
二次関数の最大値・最小値/区間(定義域)が固定されて軸が動く場合 からの続き 今回は関数が固定されて区間が動く場合の二次関数の最大値・最小値の求め方について説明します。 区間(定義域)が固定されて関数の軸が動く場合と並ん […]
二次関数の最大値・最小値/区間(定義域)が固定されて軸が動く場合
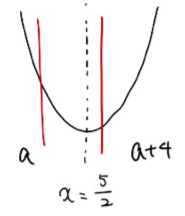
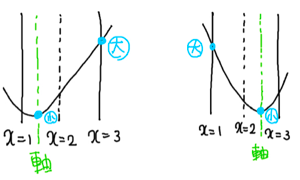
文字を含む二次関数の最大値・最小値の求め方(グラフによる場合分け)からの続き 二次関数の最大値・最小値を求める問題で最も重要なのは「定義域や関数が動くときの最大値・最小値」を求める問題です。 この問題は丸暗 […]
文字を含む二次関数の最大値・最小値の求め方(グラフによる場合分け)
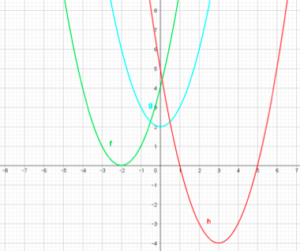
二次関数の最大値・最小値を求めるうえで、毎回必ず全ての係数が分かっているとは限りません。 ここではそのような二次関数の最大値・最小値の求め方について見ていきます。 必要な知識は平方完成くらいですので早速例題を通して見てい […]
二次関数の最大値最小値の求め方(定義域がない場合と定義域がある場合)
二次関数のグラフと平方完成、グラフの平行移動が置き換えでできる理由からの続き 二次関数では最大値と最小値を求めることをよく行います。(数IIや数IIIへ学習を進めると三次関数や四次関数などの一般の曲線でも行います) 二次 […]
二次関数のグラフと平方完成、グラフの平行移動が置き換えでできる理由
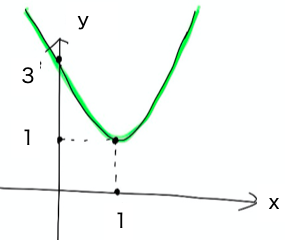
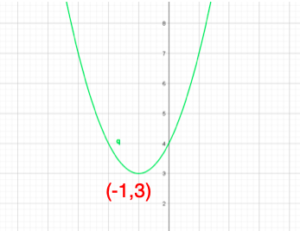
二次関数は式が与えられたときに正確にグラフの位置、形を読み取る必要があります。 しかし、y=ax2+bx+cの形のままですぐ分かることは、上に凸なグラフか、下に凸なグラフかということくらいです。 頂点の座標がすぐに分かる […]
高校数学の二次関数で平方完成を2行でやる考え方。これで二次関数の問題も時短
高校数学で最初に苦労する人が多いのは 二次関数。 そして頂点の座標を求めるため 二次間数では避けては通れないのが 平方完成。 平方完成も慣れてできるようになれば なんて言うことなくなるでしょう。 でもオーソドックスに行く […]
高校数学で一年生が迎える最初の2つの壁。二次関数と三角比の注意点と対策は?
最初の数と式はできたけど、 2次関数になってよくわからなくなった・・・ sin,cos,tanに馴染めないうちに 正弦定理とか余弦定理とか出てきて ついていけなくなった… そんな声はよく聞きますので、 似たようなつまづき […]
高校数学についていけない。考えられる2つの原因とその対策方法は?
中学までは数学できたのに、 高校生になってからわからなくなった。 高校1年生の数Ⅰまでは 何とかついていけたけど 2年生になったらついていけなくなった。 もしあなたが 似たようなことを思っていたとしても それはあなただけ […]